LBARC 1143 Mathématique Géométrie Chapitre 1 : Théorème de Thalès et proportions Examen

Questions d'examen

Voici quelques questions qui ont été posées lors d'anciens examens et qui concernent ce chapitre.

1

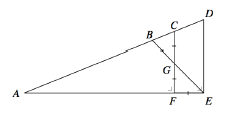
On considère la figure représentée ci-dessous, où les angles $\widehat{CFA}$ et $\widehat{DEA}$ sont droits et $|BG|=|FE|=|GF|=|CG|=1$.

  1. Déterminez les longueurs $|DE|$ et $|AF|$.

    Par Pythagore dans le triangle $GEF$, on a $|GE|=\sqrt{1+1}=\sqrt{2}$ et donc $|BE|=|BG|+|GE|=1+\sqrt{2}$.

    Par Thalès, on a

    $$\dfrac{|BG|}{|BE|}=\dfrac{|CG|}{|DE|}, \mbox{ c'est-à-dire }\dfrac{1}{1+\sqrt{2}}=\dfrac{1}{|DE|}$$

    et donc $|DE|=1+\sqrt{2}$.

    Par Thalès, on a aussi

    $$\dfrac{|CF|}{|AF|}=\dfrac{|DE|}{|AE|},\mbox{ c'est-à-dire }\dfrac{2}{|AF|}=\dfrac{1+\sqrt{2}}{|AF|+1}$$

    d'où $|AF|(\sqrt{2}-1)=2$ et $|AF|=2\sqrt{2}+2$.

  2. Déduisez-en la surface du triangle $AED$ ainsi que celle du trapèze $CDEG$.

    On déduit du point ci-dessus que $$|AE|=|AF|+|FE|=2\sqrt{2}+3.$$