LBARC 1143 Mathématique Géométrie Chapitre 1 : Théorème de Thalès et proportions Théorème de Thalès et proportions Exercices pour s'entraîner

Exercices pour s’entraîner

Entraînez-vous à résoudre les exercices suivants.

  1. On considère un triangle $ABC$ tel que $|AB|=2$ cm et $|BC|=3$ cm. Soit $P$ sur $AB$ tel que $|BP|=6$ cm. A quelle distance de $B$ faut-il marquer le point $Q$ de $BC$ pour que $PQ$ soit parallèle à $AC$ ?

    $\bullet\, $Ecrivez les proportions reliants les segments $AB$, $BP$, $BC$ et $BQ$.

    $\bullet\, $Isolez $BQ$.

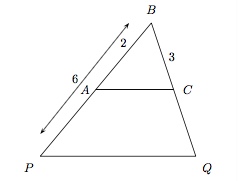
    On a $$ \begin{array}{c} \dfrac{|AB|}{|BC|}=\dfrac{|BP|}{|BQ|}\\[2mm] |BQ|=\dfrac{|BC|}{|AB|}\cdot |BP|=\dfrac{3}{2}\cdot 6=9 \end{array} $$

  2. On considère un trapèze $ABCD$ et soit $XY$ parallèle aux bases. Si $|AD|=3$ cm, $|AX|=9$ cm et $|BY|=12$ cm, calculez $|CY|$.

    $\bullet\, $Calculez la longueur du segment $DX$.

    $\bullet\, $Ecrivez les proportions reliant les segments $AX$, $DX$, $BY$ et $CY$.

    $\bullet\, $Isolez $CY$.

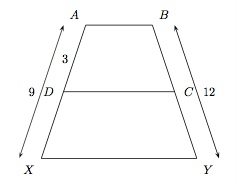
    On a $$ \begin{array}{c} |DX|=9-3=6 \\[2mm] \dfrac{|DX|}{|AX|}=\dfrac{|CY|}{|BY|}\\[2mm] |CY|=\dfrac{|DX|}{|AX|}\cdot |BY|=\dfrac{6}{9}\cdot 12=8 \end{array} $$

  3. Soint $ABCD$ un trapèze dont les bases sont $AB$ et $CD$ et tel que $|AD|=9$ cm et $|BC|=12$ cm. Par le point $M$ situé aux $3/4$ de $BD$ à partir de $B$ on trace la parallèle aux bases; elle coupe $AD$ en $P$ et $BC$ en $Q$. Calculez $|AP|$, $|PD|$ et $\frac{|BC|}{|CQ|}$.

    $\bullet\, $Ecrivez des proportions dans le triangle $ADB$.

    $\bullet\, $Déduisez-en la longueur des segments $AP$ et $PD$.

    $\bullet\, $Ecrivez des proportions dans le trapèze $ABCD$.

    $\bullet\, $Déduisez-en le rapport demandé.

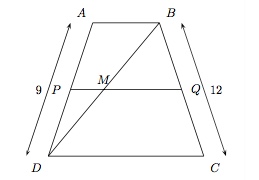
    On a $$ \begin{array}{c} \dfrac{|BM|}{|BD|}=\dfrac{3}{4}\\[2mm] \dfrac{|BM|}{|BD|}=\dfrac{|AP|}{|AD|}\\[2mm] \dfrac{3}{4}=\dfrac{|AP|}{9}\\[2mm] |AP|=\dfrac{27}{4}\\[2mm] |PD|=9-\dfrac{27}{4}=\dfrac{9}{4}\\[2mm] \dfrac{|BC|}{|CQ|}=\dfrac{|AD|}{|PD|}=\dfrac{9}{\frac{9}{4}}=4 \end{array} $$