Questions de théorie
Ces questions sont destinées à vous faire revoir la théorie de ce chapitre.
Dans la proportion $\frac{a}{b}=\frac{c}{d}$, quels sont les termes moyens ? et les termes extrèmes ?
La définition se trouve dans le syllabus, chapitre 1, section 1.
Si $a$, $b$, $c$, $d\in\mathbb{R}_0$ alors $\frac{a}{b}=\frac{c}{d}$ est une proportion où $a$ et $d$ sont les extrèmes et $b$ et $c$ sont les moyens.
Donnez une propriété des proportions.
Dans une proportion on peut permuter les moyens et permuter les extrèmes.
Dans toute proportion, le produit des moyens est égal au produit des extrèmes, c'est-à-dire $\forall a,\, b,\, c,\, d\in\mathbb{R}_0$, on a $$ \frac{a}{b}=\frac{c}{d}\Leftrightarrow ad=bc. $$
Dans quelles situations peut-on appliquer le Théorème de Thalès ?
Le Théorème de Thalès concerne un triangle coupé par une droite parallèle à l'un de ses côtés ou, plus généralement, deux triangles partageant un même sommet, ayant chacun deux côtés dans le prolongement l'un de l'autre et leur troisième côté parallèle.
Voir syllabus, chapitre 1, section 2.
Nous pouvons appliquer le Théorème de Thalès lorsque nous sommes dans une situation telle que nous avons
- deux droites sécantes,
- deux points supplémentaires sur chacune des deux droites,
- deux droites parallèles passant par ces points.
Enoncez le Théorème de Thalès, interprétez-le en français et illustrez graphiquement.
L'énoncé se trouve dans le syllabus, chapitre 1, section 2.
Théorème de Thalès : Si trois droites parallèles rencontrent deux droites $d$ et $d'$, respectivement et dans cet ordre, en $A$, $B$, $C$ et $A'$, $B'$, $C'$, alors
$$ \frac{\vert A'B'\vert}{\vert AB\vert}=\frac{\vert B'C'\vert}{\vert BC\vert}=\frac{\vert A'C'\vert}{\vert AC\vert}. $$

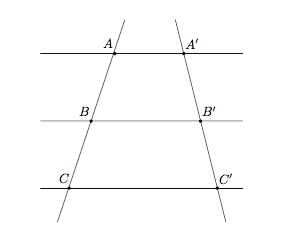
En permutant les termes moyens des fractions, on obtient d'autres égalités de rapports :$$ \frac{\vert A'B'\vert}{\vert B'C'\vert}=\frac{\vert AB\vert}{\vert BC\vert}\qquad \frac{\vert B'C'\vert}{\vert A'C'\vert}=\frac{\vert BC\vert}{\vert AC\vert} \qquad \frac{\vert A'B'\vert}{\vert A'C'\vert}=\frac{\vert AB\vert}{\vert AC\vert} $$
En français : trois droites parallèles déterminent sur deux sécantes des segments homologues proportionnels.
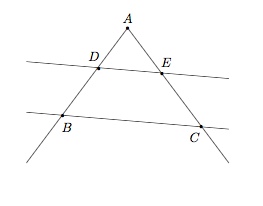
Enoncez le Théorème de Thalès dans le cas particulier du triangle.
Dans le cas du triangle, on a $A=A'$.
Dans le cas particulier du triangle, on obtient les égalités suivantes :
$$ \frac{\vert AD\vert}{\vert DB\vert}=\frac{\vert AE\vert}{\vert EC\vert}\qquad \frac{\vert AD\vert}{\vert AB\vert}=\frac{\vert AE\vert}{\vert AC\vert} \qquad \frac{\vert DB\vert}{\vert AB\vert}=\frac{\vert EC\vert}{\vert AC\vert} $$