Exercices pour s’entraîner
Entraînez-vous à résoudre les exercices suivants.
-
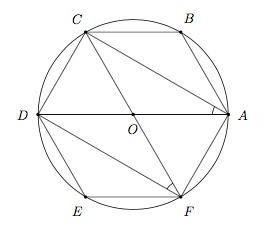
Dans la figure ci-dessus, donnez 3 angles qui ont la même amplitude que $\widehat{DEC}$.
Des angles inscrits qui interceptent le même arc de cercle ont même amplitude.
Les angles $\widehat{DEC}$, $\widehat{DFC}$, $\widehat{DAC}$ et $\widehat{DBC}$ interceptent le même arc $DC$. Ils ont donc même amplitude.
-

Dans la figure ci-dessus, donnez 3 angles dont l'amplitude vaut la moitié de celle de $\widehat{DOF}$.
Dans un cercle, l'amplitude de l'angle au centre vaut le double de l'amplitude de l'angle inscrit qui intercepte le même arc.
L'angle $\widehat{DOF}$ est un angle au centre qui intercepte l'arc de cercle $DF$. Les angles $\widehat{DCF}$, $\widehat{DBF}$ et $\widehat{DAF}$ interceptent le même arc $DF$. Leur amplitude vaut donc la moitié de celle de $\widehat{DOF}$.
-

Dans la figure ci-dessus, comment sont les angles $\widehat{ECB}$ et $\widehat{BAE}$ ?
Ces triangles sont inscrits dans un demi-cercle.
Les triangles $ECB$ et $BAE$ sont inscrits dans des demi-cercles de diamètre $EB$. Ce sont donc des triangles rectangles et donc $\widehat{ECB}=\widehat{BAE}=90^{\circ}$.