Exercices pour s’entraîner
Entraînez-vous à résoudre les exercices suivants.
-
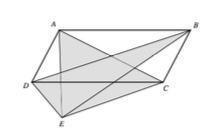
On considère le parallélogramme $ABCD$ ci-dessous. Soit $G$ le centre de gravité du triangle $AEC$. Démontrez que $G$ est le centre de gravité du triangle $BDE$.
Le centre de gravité d'un triangle se trouve à l'intersection des médianes, à deux-tiers de chacun des sommets.
Les diagonales d'un parallélogramme se coupent en leur milieu.
Soit $O$ l'intersection des diagonales du parallélogramme, $O$ est donc le milieu du côté $AC$ et le milieu du côté $BD$.
$EO$ est une médiane du triangle $AEC$, le centre de gravité $G$ se trouve sur $EO$ aux 2/3 de $E$.
$EO$ est aussi une médiane du triangle $BDE$ et puisque $G$ se trouve sur $EO$ aux 2/3 de $E$, on en déduit que $G$ est le centre de gravité du triangle $BDE$.
-
On considère la figure ci-dessous.
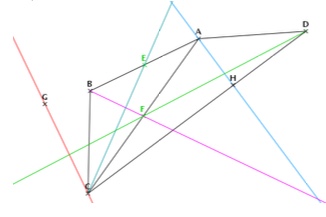
Déterminez la hauteur issue de $A$ dans le triangle $ADC$ et la hauteur issue de $C$ dans le triangle $ABC$.
Dans le triangle $ABC$, déterminez la nature des droites $CE$, $CG$ et $BF$.
Dans le triangle $ADC$, déterminez la nature des droites $DF$ et $AH$.
Les définitions se trouvent dans le syllabus, chapitre 3, section 2.
$AH$ est la hauteur issue de $A$ dans le triangle $ADC$ et $CG$ est la hauteur issue de $C$ dans le triangle $ABC$.
Dans le triangle $ABC$, $CE$ est une médiane, $CG$ est une hauteur, $BF$ est à la fois une médiane, une médiatrice et une hauteur.
Dans le triangle $ADC$, $DF$ est une médiane et $AH$ est une hauteur.
-
Construisez un triangle isocèle $DEF$ tel que $|ED|=6$, $|DF|=8$ et $|EF|=8$. Tracez ensuite $AB$ médiatrice du segment $ED$.
Le point $F$ appartient-il à la droite $AB$ ? Justifiez.
La droite $AB$ est-elle une médiane du triangle $EDF$ ? Justifiez.
La droite $AB$ est-elle une hauteur du triangle $EDF$ ? Justifiez.
Les définitions se trouvent dans le syllabus, chapitre 3, section 2.
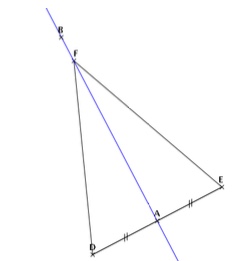
Le point $F$ appartient à la droite $AB$. En effet, la médiatrice $AB$ contient tous les points situés à égale distance des sommets $D$ et $E$. Comme le triangle $DEF$ est isocèle, le point $F$ est à égale distance des points $D$ et $E$, il est donc sur la médiatrice $AB$.
La droite $AB$ étant une médiatrice, elle coupe le côté $DE$ en deux segments de même longueur. $A$ est donc au milieu du côté $DE$ et comme le sommet $F$ appartient à la droite $AB$ on en déduit que cette droite est aussi une médiane.
La droite $AB$ étant une médiatrice, elle est perpendiculaire au côté $DE$. Comme le sommet $F$ appartient à la droite $AB$ on en déduit que cette droite est aussi une hauteur.