Exercices résolus
Voici quelques exemples d'exercices résolus en détails.
-
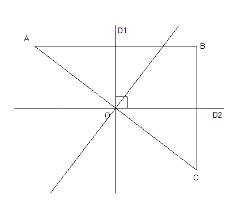
Soit $D1$ et $D2$ deux droites perpendiculaires qui se coupent en $O$ et $A$ un point du plan.
Le point $B$ est le symétrique de $A$ par rapport à $D1$ et le point $C$ est le symétrique de $B$ par rapport à $D2$.
Montrez que le point $O$ appartient à la médiatrice du segmant $AC$.
Puisque $B$ est le symétrique de $A$ par rapport à $D1$, la droite $D1$ coupe $AB$ en deux segments de même longueur. De même puisque $C$ est le symétrique de $B$ par rapport à $D2$, la droite $D2$ coupe $BC$ en deux segments de même longueur. Comme $D1$ est perpendiculaire à $AB$ et $D2$ est perpendiculaire à $BC$ on en déduit que $D1$ et $D2$ sont des médiatrices du triangle $ABC$.
Or les médiatrices d'un triangle se coupent en un point qui est le centre du cercle circonscrit au triangle. Le point $O$ est donc le centre du cercle circonscrit et donc $|OA|=|OC|$, ce qui prouve que $O$ appartient à la médiatrice du segment $AC$.