Exercices pour s’entraîner
Entraînez-vous à résoudre les exercices suivants.
-
Calculez la longueur de la diagonale du cube de côté $c=10$.
Utilisez le Théorème de Pythagore dans deux plans différents : dans une face du cube et dans un plan qui coupe le cube en diagonale.
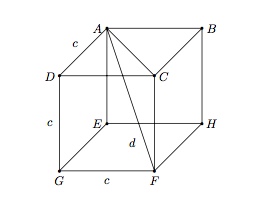
La diagonale du cube de côté $c=10$ est la diagonale du rectangle $ACFE$ et est telle que $$d^2=\vert AC\vert^2+\vert CF\vert^2=\vert AC\vert^2+c^2.$$
D'autre part, $AC$ est la diagonale du carré $ABCD$ et donc $$\vert AC\vert^2=c^2+c^2=2c^2.$$
Finalement on obtient $d^2=2c^2+c^2=3c^2$ et donc la longueur de la diagonale du cube est $d=\sqrt{3}\, c=10\sqrt{3}$.
-
Calculez la hauteur d'un triangle équilatéral de côté $c=2$.
Dans un triangle équilatéral, la hauteur est aussi médiane.
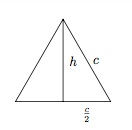
Dans un triangle équilatéral, la hauteur est aussi une médiane, elle coupe donc le côté en deux parties égales.
On déduit du Théorème de Pythagore que
$$ \begin{array}{c} h^2+\left(\dfrac{c}{2}\right)^2=c^2 \\ h^2=\dfrac{3}{4}c^2 \\ h=\dfrac{\sqrt{3}}{2}c \end{array} $$
La hauteur d'un triangle équilatéral de côté $c=2$ vaut donc $h=\dfrac{\sqrt{3}}{2}c=\sqrt{3}$.
-
On considère le cercle $\mathcal{C}$ de centre $C$ et de rayon $2$ cm et le cercle $\mathcal{C'}$ de centre $C'$ et de rayon $4$ cm. La droite $t$, tangente commune aux deux cercles, est tangente à $\mathcal{C}$ en $A$ et à $\mathcal{C'}$ en $A'$. Sachant que la distance entre les centres $C$ et $C'$ est de $5$ cm, calculez la distance entre $A$ et $A'$.
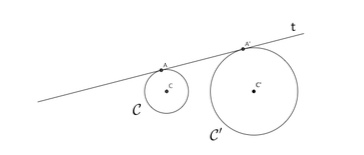
La tangente en un point d'un cercle est perpendiculaire à son rayon en ce point.
Puisque la tangente en un point d'un cercle est perpendiculaire à son rayon en ce point, on a $t\perp AC$ et $t\perp A'C'$. On en déduit que $AC$ et $A'C'$ sont parallèles.
Traçons le rectangle $AA'XC$. On a $|AC|=|A'X|=2$, donc $|XC'|=|A'C'|-|A'X|=4-2=2$.
Puisque $|CC'|=5$ on déduit du Théorème de Pythagore que $$|CX|^2=|CC'|^2-|XC'|^2=25-4=21.$$
Finalement, $|AA'|=|CX|=\sqrt{21}$.
-
On considère le triangle rectangle $ABC$ dont l'hypoténuse $AB$ vaut $4\sqrt{3}$ et dont l'angle en $B$ vaut $60^{\circ}$. Déterminez la longueur des deux autres côtés.
- Commencez par déterminer la longueur d'un des côtés en utilisant les formules de trigonométrie dans un triangle rectangle.
- Utilisez ensuite le Théorème de Pythagore pour en déduire la longueur du dernier côté.
On calcule $\sin{60^{\circ}}=\dfrac{|AC|}{|AB|}=\dfrac{|AC|}{4\sqrt{3}}=\dfrac{\sqrt{3}}{2}$ d'où $|AC|=\dfrac{4\sqrt{3}\cdot\sqrt{3}}{2}=6$. On déduit ensuite du Théorème de Pythagore que $|BC|^2=|AB|^2-|AC|^2=48-36=12$ et donc $|BC|=2\sqrt{3}$.
-
Déterminez le rayon du cercle inscrit dans un triangle rectangle dont les côtés de l'angle droit valent $3$ et $4$.
- Déterminez la longueur de l'hypoténuse.
- Découpez le triangle en 3 triangles dont la hauteur est le rayon du cercle et donnez l'aire de ces 3 triangles.
- Donnez l'aire du triangle de départ et comparez avec la somme des aires des 3 triangles ci-dessus.
Soit un triangle rectangle $ABC$ rectangle en $C$ tel que $|AC|=4$, $|BC|=3$. La longueur de l'hypoténuse vaut $|AB|=\sqrt{3^2+4^2}=\sqrt{25}=5$. Soit $K$ le centre du cercle inscrit et $r$ son rayon.
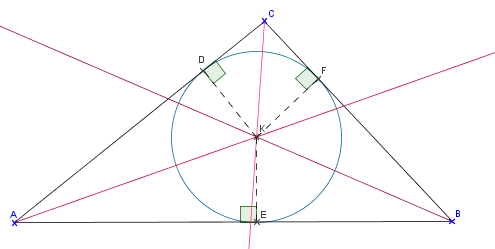
On découpe $ABC$ en 3 triangles $AKB$, $BKC$ et $AKC$. La somme des aires de ces 3 triangles vaut $$\dfrac{|AB|\cdot r}{2}+\dfrac{|BC|\cdot r}{2}+\dfrac{|AC|\cdot r}{2}=\dfrac{r\, (5+3+4)}{2}=\dfrac{12r}{2}=6r.$$
L'aire du triangle rectangle $ABC$ vaut $\dfrac{|AC|\cdot |BC|}{2}=\dfrac{12}{2}=6$.
On en déduit que $6r=6$ et donc $r=1$.
-
Dans la figure ci-dessous, si $a=12$ et $b=20$, déterminez $c$, $d$ et $h$.
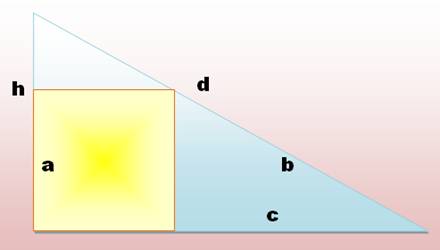
- Utilisez le Théorème de Pythagore pour trouver c.
- Utilisez ensuite le Théorème de Thalès pour en déduire h.
- Finalement, déduisez d du Théorème de Pythagore.
On déduit du Théorème de Pythagore que $c^2=b^2-a^2=400-144=256$ et donc $c=16$.
Du Théorème de Thalès, on déduit les égalités
$$ \begin{array}{c} \dfrac{h}{a+c}=\dfrac{a}{c}\\ \dfrac{h}{28}=\dfrac{12}{16}\\ h=\dfrac{28\cdot 3}{4}\\ h=21 \end{array} $$
Finalement, par Pythagore on a $d^2=h^2+(a+c)^2=441+784=1225$ et donc $d=35$.