LBARC 1143 Mathématique Géométrie Chapitre 3 : Les triangles Triangles semblables Exercices pour s'entraîner

Exercices pour s’entraîner

Entraînez-vous à résoudre les exercices suivants.

  1. Des triangles dont les côtés mesurent respectivement 22 cm, 48cm, 40 cm et 24 cm, 20 cm, 11 cm sont-ils semblables.  Si oui, donnez le rapport de proportion entre les côtés.

    Dans les triangles semblables, les côtés homologues sont proportionnels.

    Ces triangles sont semblables car $\dfrac{22}{11}=\dfrac{48}{24}=\dfrac{40}{20}=2$.  Le rapport de proportion est $2$.

  2. Deux triangles possèdent chacun un angle de $35^{\circ}$ compris entre des côtés mesurant respectivement 10 cm et 32 cm pour le premier, 15 cm et 48 cm pour le second.  Ces triangles sont-ils semblables ?  Si oui, précisez le rapport de proportion.

    Deux triangles sont semblables s'ils ont un angle de même amplitude dont les côtés correspondants sont proportionnels.

    Ces triangles sont semblables car ils ont un angle de même amplitude compris entre des côtés homologues proportionnels : $\dfrac{10}{15}=\dfrac{32}{48}=\dfrac{2}{3}$.  Le rapport de proportion est $\dfrac{2}{3}$.

  3. Deux triangles $ABC$ et $A'B'C'$ sont rectangles en $A$ et $A'$ et tels que $|AB|=3$, $|AC|=4$, $|A'B'|=9$ et $|B'C'|=12$.  Ces triangles sont-ils semblables ?

    Deux triangles sont semblables s'ils ont un angle de même amplitude dont les côtés correspondants sont proportionnels.

    Ces triangles ne sont pas semblables.  En effet, par Pythagore dans le triangle $ABC$ on obtient $|BC|=\sqrt{3^2+4^2}=\sqrt{25}=5$ et $\dfrac{|AB|}{|BC|}=\dfrac{3}{5}\neq\dfrac{9}{12}=\dfrac{|A'B'|}{|B'C'|}$.

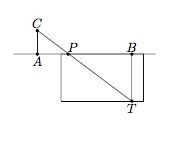
  4. Dans la situation ci-dessus, les triangles $ACP$ et $PBT$ sont-il semblables ?

    Deux triangles sont semblables s'ils ont deux angles correspondants de même amplitude.

    Les triangles $ACP$ et $PBT$ sont semblables car ils ont leurs 3 angles de même amplitude deux à deux : $\widehat{CAP}=\widehat{PBT}=90^{\circ}$ et $\widehat{CPA}=\widehat{BPT}$ car ils sont opposés par le sommet.  Les angles $\widehat{ACP}$ et $\widehat{BTP}$ ont donc aussi même amplitude.

  5. Dans la figure ci-dessous, déterminez deux triangles semblables au triangle $ADC$.

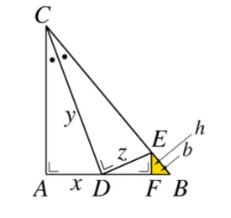
    Deux triangles sont semblables s'ils ont deux angles correspondants de même amplitude.

    Les triangles $ADC$ et $DCE$ sont semblables car ils ont leurs angles de même amplitude deux à deux : $\widehat{CAD}=\widehat{CDE}=90^{\circ}$, $\widehat{ACD}=\widehat{DCE}$ par l'énoncé et donc $\widehat{ADC}=\widehat{DEC}$.

    Les triangles $ADC$ et $FED$ sont semblables car ils ont leurs angles de même amplitude deux à deux : $\widehat{CAD}=\widehat{DFE}=90^{\circ}$, $\widehat{ADC}+\widehat{EDF}=90^{\circ}=\widehat{FED}+\widehat{EDF}$ et donc $\widehat{ADC}=\widehat{FED}$.  On en déduit que $\widehat{ACD}=\widehat{FDE}$.