Exercices résolus
Voici quelques exemples d'exercices résolus en détails.
-
Supposons qu'une personne de 1,80 m souhaite déterminez la hauteur d'un pont au dessus d'une rivière.
Commençons par représenter la situation
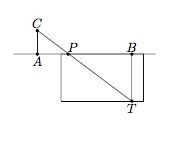

La personne se tient en $A$ à un bout du pont et regarde le point $T$ de la rivière en dessous de $B$. Il note $P$ l'endroit où sa vision rencontre le pont. Ce point $P$ permet de former deux triangles : les triangles $APC$ et $BPT$.
Ces deux triangles sont semblables car ils ont deux angles égaux : un angle droit (respectivement en $A$ et en $B$) et les deux angles en $P$. On peut maintenant calculer la hauteur du pont en utilisant les relations dans les triangles semblables : si $|AP| $ vaut 3 m et si $|PB| $ vaut 12 m, alors
$$ \frac{|AC|}{|BT|}=\frac{|AP|}{|PB|} = \frac{3}{12}. $$Donc $|BT|= |AC|. \frac{12}{3}= (1,8). 4 = 7,2$ m.