Questions d'examen
Voici quelques questions qui ont été posées lors d'anciens examens et qui concernent ce chapitre.
Donnez les solutions de l'équation $\cos{x}=-\sin{\frac{x}{2}}$ dans $[0,2\pi]$.
L'équation peut encore s'écrire
$$\cos{x}=\sin{\left(-\frac{x}{2}\right)}$$
$$\cos{x}=\cos{\left(\frac{\pi}{2}+\frac{x}{2}\right)}$$
On en déduit
$\bullet\, x=\frac{\pi}{2}+\frac{x}{2}+2k\pi$ et donc $x=\pi+4k\pi$ avec $k\in\mathbb{Z}$,
$\bullet\, x=-(\frac{\pi}{2}+\frac{x}{2})+2k\pi$ et donc $x=-\frac{\pi}{3}+\frac{4k\pi}{3}$ avec $k\in\mathbb{Z}$.
Parmi ces solutions, la seule à être dans $[0,2\pi]$ est $x=\pi$.
Montrez que pour tout $x\in\mathbb{R}$, on a
$$\cos{(3\pi-x)}+\cos{\left(\frac{\pi}{2}+x\right)}+\sin{\left(\frac{-3\pi}{2}-x\right)}=-\sin{x}.$$
On a
$$\cos{(3\pi-x)}=\cos{(2\pi+\pi-x)}=\cos{(\pi-x)}=-\cos{x},$$
$$\cos{\left(\frac{\pi}{2}+x\right)}=-\sin{x}$$
et
$$\sin{\left(\frac{-3\pi}{2}-x\right)}=\cos{\left(\frac{\pi}{2}-\left(\frac{-3\pi}{2}-x\right)\right)}=\cos{(2\pi+x)}=\cos{x}.$$
On en déduit \begin{array}{rcl} \cos{(3\pi-x)}+\cos{\left(\frac{\pi}{2}+x\right)}+\sin{\left(\frac{-3\pi}{2}-x\right)}&=&-\cos{x}-\sin{x}+\cos{x}\\ &=&-\sin{x}. \end{array}
Vous commandez à une compagnie de bois un poteau de $75$ mètres de hauteur. Un bucheron pense avoir repéré un arbre assez haut pour satisfaire la commande. L'arbre est situé sur une colline et l'angle qu'il fait par rapport au plan de la colline est de $105^{\circ}$. Le bucheron, placé sur la colline à $100$ mètres en contrebas de l'arbre, voit le sommet de son tronc sous un angle de $30^{\circ}$. L'arbre est-il bien celui qu'il faut couper pour satisfaire la commande ? Justifiez et représentez la situation.
La situation peut être représentée par le schéma suivant
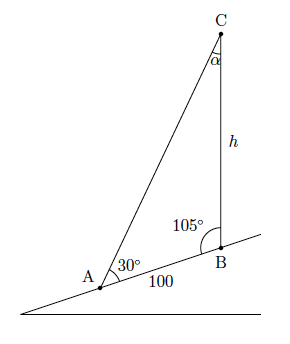
où $h$ représente la hauteur du tronc et $A$ la position du bucheron.
On calcule $\alpha=180^{\circ}-105^{\circ}-30^{\circ}=45^{\circ}$.
Par la Règle des sinus dans le triangle $ABC$, on a
$$\dfrac{h}{\sin{30^{\circ}}}=\dfrac{100}{\sin{45^{\circ}}},$$
$$h=100\cdot \dfrac{\sin{30^{\circ}}}{\sin{45^{\circ}}}=100\cdot \dfrac{1}{2}\cdot \dfrac{2}{\sqrt{2}}=50\cdot\sqrt{2}.$$
Or $50\cdot\sqrt{2}\simeq 50\cdot 1,4142=\dfrac{141,42}{2}<71$.
Le tronc mesure moins de $71$ mètres. Cet arbre ne convient donc pas pour la commande.
En utilisant le Théorème de la médiane, calculez la longueur d'une médiane d'un triangle équilatéral de côté $a$.
Soit $a$ la longueur d'un côté du triangle et $m$ la longueur de la médiane.
On a par le Théorème de la médiane :
$$a^2+a^2=2m^2+\frac{a^2}{2}$$
$$2m^2=2a^2-\frac{a^2}{2}$$
$$2m^2=\frac{3}{2}a^2$$
et donc $m=\frac{\sqrt{3}}{2}a$.