LBARC 1143 Mathématique Géométrie Chapitre 4 : Trigonométrie Nombres trigonométriques Exercices résolus

Exercices résolus

Voici quelques exemples d'exercices résolus en détails.

  1. Si $\alpha$ est un angle aigu et $\cos \alpha = \frac{3}{4}$, calculez les valeurs des autres nombres trigonométriques de $\alpha$.

    On peut représenter la situation par un triangle rectangle dont le côté adjacent à $\alpha$ vaut $3$ et l'hypoténuse vaut $4$. 

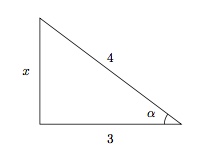
    Le côté opposé à $\alpha$ vaut donc $x=\sqrt{4^2-3^2}=\sqrt{7}$.  On en déduit

    $\sin{\alpha}=\dfrac{\sqrt{7}}{4}$

    $\cos{\alpha}=\dfrac{3}{4}$

    $\mbox{tg }\alpha=\dfrac{\sin{\alpha}}{\cos{\alpha}}=\dfrac{\sqrt{7}}{3}$

    $\mbox{cotg }\alpha=\dfrac{\cos{\alpha}}{\sin{\alpha}}=\dfrac{3}{\sqrt{7}}=\dfrac{3\sqrt{7}}{7}$

  2. En utilisant un triangle isocèle, calculez les valeurs des nombres trigonométriques dans angles $\dfrac{\pi}{5}$ et $\dfrac{\pi}{10}$.

    En utilisant un triangle isocèle $ABC$ dont l'angle entre les deux côtés égaux vaut $\dfrac{\pi}{5}$, on peut déterminer les valeurs de $\cos{\frac{\pi}{5}}$ et $\sin{\frac{\pi}{10}}$.

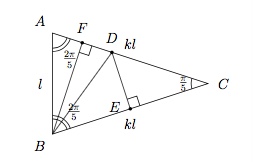
    Notons $|AB|=l$ et $|BC|=|AC|=kl$. Traçons $BD$ bissectrice de l'angle $\widehat{B}$.

    On a $\widehat{ABD}=\dfrac{\pi}{5}$, $\widehat{BAD}=\dfrac{2\pi}{5}$ et donc $\widehat{ADB}=\dfrac{2\pi}{5}$. On en déduit que le triangle $ABD$ est isocèle et donc $|BD|=l$.

    Comme $\widehat{CBD}=\dfrac{\pi}{5}$, le triangle $BDC$ est aussi isocèle et on a aussi $|DC|=l$. On en déduit $|AD|=kl-l=l(k-1)$.

    Les triangles $ABD$ et $ABC$ étant semblables, on a $$\dfrac{|AD|}{|AB|}=\dfrac{|AB|}{|BC|}$$ $$\dfrac{l(k-1)}{l}=\dfrac{l}{kl}$$ et donc $k^2-k-1=0$. On en déduit $k=\dfrac{1+\sqrt{5}}{2}$.

    Traçons $DE$ la hauteur relative au côté $BC$ dans le triangle $BDC$. On a $$\cos{\frac{\pi}{5}}=\dfrac{|CE|}{|DC|}=\dfrac{\frac{kl}{2}}{l}=\dfrac{k}{2}=\dfrac{1+\sqrt{5}}{4}.$$

    Traçons $BF$ la hauteur relative au côté $AD$ dans le triangle $ABD$. On a $$\sin{\frac{\pi}{10}}=\dfrac{|AF|}{|AB|}=\dfrac{\frac{l(k-1)}{2}}{l}=\dfrac{k-1}{2}=\dfrac{\sqrt{5}-1}{4}.$$

    On en déduit les valeurs de $\sin{\frac{\pi}{5}}$ et $\cos{\frac{\pi}{10}}$ en utilisant la formule fondamentale par exemple.