Questions de théorie

Le cercle trigonométrique est un cercle de rayon 1 centré à l'origine. On mesure l'angle $\alpha$ à partir de l'axe horizontal; $\alpha$ est positif dans le sens anti-horlogique et négatif dans le sens des aiguilles d'une montre.

En appliquant le Théorème de Pythagore dans le triangle rectangle $OAB$, on obtient la formule fondamentale suivante : $$\sin^2\alpha+\cos^2\alpha=1.$$

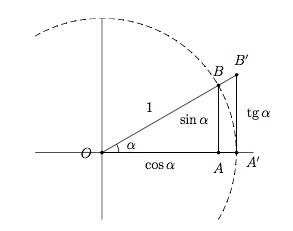
Les triangles $OAB$ et $OA'B'$ sont semblables et par les propriétés des triangles semblables, on a donc $$\frac{|A'B'|}{|OA'|}=\frac{|AB|}{|OA|}$$ c'est-à-dire  $$\mbox{tg }\alpha=\frac{\sin\alpha}{\cos\alpha}.$$

Remarquons que le nombre $\mbox{tg }\alpha$ n'est défini que pour $\alpha\neq\frac{\pi}{2}+k\pi$, $k\in \mathbb{Z}$.

Les triangles $OAB$ et $OA'B'$ sont semblables et par les propriétés des triangles semblables, on a donc $$\frac{|OA'|}{|A'B'|}=\frac{|OA|}{|AB|}$$ c'est-à-dire $$\mbox{cotg }\alpha=\frac{1}{\mbox{tg }\alpha}=\frac{\cos\alpha}{\sin\alpha},$$

où $\alpha\neq k\pi$, $k\in \mathbb{Z}$.

Dans le triangle rectangle $OAB$ on a $$\dfrac{|AB|}{|OB|}=\frac{\sin\alpha}{1}=\sin\alpha,$$ d'où $$\sin{\alpha}=\dfrac{\mbox{côté opposé à }\alpha}{\mbox{hypoténuse}}.$$

Dans le triangle rectangle $OAB$ on a $$\dfrac{|OA|}{|OB|}=\frac{\cos\alpha}{1}=\cos\alpha,$$ d'où $$\cos\alpha=\displaystyle\frac{\mbox{côté adjacent à }\alpha}{\mbox{hypoténuse}}.$$

Vu que $\mbox{tg }\alpha=\frac{\sin\alpha}{\cos\alpha}$, on obtient $$\mbox{tg }\alpha=\displaystyle\frac{\sin\alpha}{\cos\alpha}=\frac{\mbox{côté opposé à }\alpha}{\mbox{côté adjacent à }\alpha}.$$

On considère un triangle rectangle $ABC$ dont les deux autres angles valent $\dfrac{\pi}{6}$ et $\dfrac{\pi}{3}$.

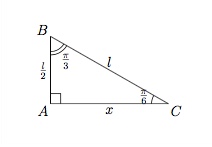
Soit $|BC|=l$. Ce triangle étant la moitié d'un triangle équilatéral, on a $|AB|=\dfrac{l}{2}$ et notons $|AC|=x$. On déduit du Théorème de Pythagore que $$x^2+\left(\dfrac{l}{2}\right)^2=l^2$$ $$x^2=\dfrac{3}{4} l^2$$ et donc$$x=\dfrac{\sqrt{3}}{2} l.$$  On en déduit $$ \sin{\frac{\pi}{6}}=\dfrac{\frac{l}{2}}{l}=\dfrac{1}{2},$$ $$\cos{\frac{\pi}{6}}=\dfrac{x}{l}=\dfrac{\sqrt{3}}{2},$$ et $$\mbox{tg }{\frac{\pi}{6}}=\dfrac{\sin{\frac{\pi}{6}}}{\cos{\frac{\pi}{6}}}=\dfrac{\sqrt{3}}{3}.$$

De même $$\sin{\frac{\pi}{3}}=\dfrac{x}{l}=\dfrac{\sqrt{3}}{2},$$ $$\cos{\frac{\pi}{3}}=\dfrac{\frac{l}{2}}{l}=\dfrac{1}{2},$$ et $$\mbox{tg }{\frac{\pi}{3}}=\dfrac{\sin{\frac{\pi}{3}}}{\cos{\frac{\pi}{3}}}=\sqrt{3}.$$

On considère un triangle rectangle $ABC$ dont les deux autres angles valent $\dfrac{\pi}{4}$. Ce triangle est isocèle.

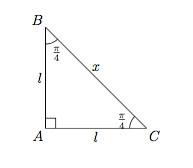
Soit $|AB|=|AC|=l$ et notons $|BC|=x$. On déduit du Théorème de Pythagore que $$l^2+l^2=x^2$$ et donc $$x=\sqrt{2}l.$$ On en déduit $$\sin{\frac{\pi}{4}}=\dfrac{l}{\sqrt{2}l}=\dfrac{\sqrt{2}}{2},$$ $$\cos{\frac{\pi}{4}}=\dfrac{l}{\sqrt{2}l}=\dfrac{\sqrt{2}}{2},$$ et $$\mbox{tg }{\frac{\pi}{4}}=\dfrac{\sin{\frac{\pi}{4}}}{\cos{\frac{\pi}{4}}}=1.$$

Dans un cercle trigonométrique, deux angles opposés sont représentés par deux points du cercle symétriques par rapport à l'axe $OX$.

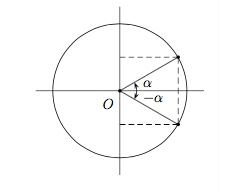
On a $$\sin ( -\alpha) = - \sin \alpha,$$ $$\cos ( -\alpha) = \cos \alpha,$$ $$\mbox{tg } ( -\alpha) = - \mbox{tg } \alpha,$$ $$\mbox{cotg }( -\alpha) = - {\rm cotg }\: \alpha.$$

Dans un cercle trigonométrique, deux angles complémentaires sont représentés par deux points du cercle symétriques par rapport à la droite $y=x$.

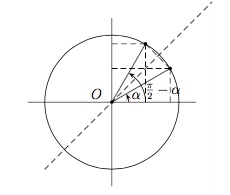
On a $$\sin ({\pi \over 2} -\alpha) = \cos \alpha, $$ $$\cos ({\pi \over 2} -\alpha) = \sin \alpha,$$ $$\mbox{tg }({\pi \over 2} -\alpha) =\mbox{cotg } \alpha,$$ $$\mbox{cotg }({\pi \over 2} -\alpha) =\mbox{tg } \alpha.$$

Dans un cercle trigonométrique, deux angles supplémentaires sont représentés par deux points du cercle symétriques par rapport à l'axe $OY$.

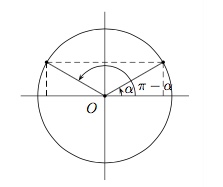
On a $$\sin (\pi -\alpha) = \sin \alpha,$$ $$\cos (\pi -\alpha) = - \cos \alpha,$$ $$\mbox{tg }(\pi -\alpha) = - \mbox{tg }\alpha,$$ $$\mbox{cotg }(\pi -\alpha) = -\mbox{cotg }\alpha.$$

Dans un cercle trigonométrique, deux angles anti-supplémentaires sont représentés par deux points du cercle symétriques par rapport à l'origine $O$.

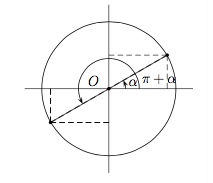
On a $$\sin (\pi +\alpha) = - \sin \alpha,$$ $$\cos (\pi +\alpha) = - \cos \alpha,$$ $$\mbox{tg }(\pi +\alpha) = \mbox{tg }\alpha,$$ $$\mbox{cotg }(\pi +\alpha) = \mbox{cotg }\alpha.$$

$\sin (2a) = 2 \sin a \cos a$

$\cos (2a) = \cos ^2 a - \sin ^2 a = 1 - 2 \sin ^2 a = 2\cos ^2 a - 1$

$\sin ^ 2 a =\dfrac{1 - \cos (2a)}{2}$

$\cos ^ 2 a = \dfrac{1 + \cos (2a)}{2}$

$1+\mbox{tg }^2{a} =\dfrac {1}{\cos^2 a}$

$\sin{(a+b)}=\sin a \cos b + \sin b \cos a$

$\cos{(a+b)}=\cos a \cos b- \sin b \sin a$

$\sin{(a-b)}=\sin a \cos b - \sin b \cos a$

$\cos{(a-b)}=\cos a \cos b + \sin b \sin a$

$\sin{a}+\sin{b}=2 \sin {(\frac{a+b}{2})} \cos {(\frac{a-b}{2})}$

$\cos{a}+\cos{b}=2 \cos {(\frac{a+b}{2})} \cos {(\frac{a-b}{2})}$

$\sin{a}-\sin{b}=2 \sin {(\frac{a-b}{2})} \cos {(\frac{a+b}{2})}$

$\cos{a}-\cos{b}=-2 \sin {(\frac{a-b}{2})} \sin{(\frac{a+b}{2})}$