Exercices pour s’entraîner
Entraînez-vous à résoudre les exercices suivants.
-
Déterminez la hauteur d'un chêne sachant que l'angle d'élévation de sa cîme passe de $30$ degrés à $75$ degrés lorsque l'observateur se rapproche de 30 mètres du pieds de l'arbre.
On peut représenter la situation par le shéma suivant
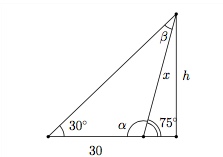
$\bullet\, $ déterminez les angles
$\bullet\, $ utilisez la Règle des sinus pour trouver $x$
$\bullet\, $ utilisez les formules dans un triangle rectangle pour trouver $h$
On peut représenter la situation par le shéma suivant

Commençons par déterminer les angles : $\alpha=180^{\circ}-75^{\circ}=105^{\circ}$, $\beta=180^{\circ}-\alpha-30^{\circ}=45^{\circ}$.
Déterminons $x$ en utilisant la Règle des sinus. On a
$$\frac{\sin{30^{\circ}}}{x}=\frac{\sin{\beta}}{30}$$
d'où
$$x=\frac{\sin{30^{\circ}}}{\sin{45^{\circ}}}\cdot 30=\frac{1}{2}\cdot\frac{2}{\sqrt{2}}\cdot 30=\frac{30}{\sqrt{2}}$$
On en déduit que
$$h=x\sin{75^{\circ}}=\frac{30}{\sqrt{2}}\sin{75^{\circ}}.$$
Or$$ \begin{array}{rcl} \sin{75^{\circ}}&=&\sin{(45^{\circ}+30^{\circ})}\\ &=&\sin{45^{\circ}}\cos{30^{\circ}}+\sin{30^{\circ}}\cos{45^{\circ}}\\ &=&\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\\ &=&\dfrac{1}{4}(\sqrt{6}+\sqrt{2}) \end{array} $$
et donc $h=\dfrac{30}{\sqrt{2}}\sin{75^{\circ}}=\dfrac{30}{\sqrt{2}}\cdot\dfrac{1}{4}(\sqrt{6}+\sqrt{2})=\dfrac{15}{2}(\sqrt{3}+1)\simeq 20,49$ mètres.
-
Deux points $P$ et $Q$ sont sur les faces opposées d'un bâtiment, à la hauteur du sol. Pour calculer la distance entre ces deux points, un géomètre choisit un point $R$ qui est distant de 90 m de $P$ et de 131 m de $Q$. L'angle $\widehat{PRQ}$ a une mesure de $37,66^{\circ}$. Calculez la distance entre $P$ et $Q$.
Utilisez la Règle des cosinus dans le triangle $PQR$.
Soit $d$ la distance entre $P$ et $Q$. On déduit de la Règle des cosinus que
$$d^2=90^2+131^2-2\cdot 90\cdot 131\cdot \cos{37,66^{\circ}}\simeq 6593,88$$
et donc $d=\sqrt{6593,88}\simeq 81,2$ mètres.
-
On doit mesurer la largeur d'une rivière au pied d'un arbre $A$ qui se trouve sur l'autre rive, inaccessible. Pour cela, on mesure en deux points $P$ et $Q$ les angles $\widehat{APQ}$ et $\widehat{AQP}$. Ces deux angles sont respectivement de $60^{\circ}$ et $75^{\circ}$. Sachant que les points $P$ et $Q$ sont distants de $50$ m l'un de l'autre et se trouvent à $10$ m de la rive, calculez la largeur de la rivière. Représentez la situation.
On peut représenter la situation par le shéma suivant
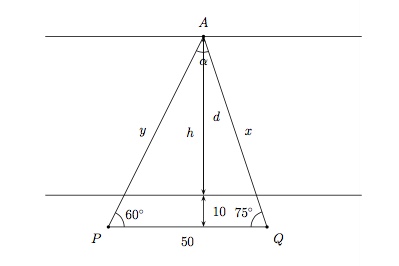
$\bullet\, $ utilisez la Règle des sinus dans le triangle $APQ$ pour trouver $x$
$\bullet\, $ travaillez dans le triangle rectangle pour en déduire $h$
$\bullet\, $ déduisez-en $d$
On peut représenter la situation par le shéma suivant

On a $\alpha=180^{\circ}-60^{\circ}-75^{\circ}=45^{\circ}$.
Recherche de $x$ par la Règle des Sinus dans le triangle $APQ$ :
$$\dfrac{x}{\sin{60^{\circ}}}=\dfrac{50}{\sin{45^{\circ}}},$$
$$x=50\cdot\dfrac{\sin{60^{\circ}}}{\sin{45^{\circ}}}=50\cdot\dfrac{\sqrt{3}}{2}\cdot\dfrac{2}{\sqrt{2}}=50\cdot\dfrac{\sqrt{3}}{\sqrt{2}}.$$
Recherche de $h$ :
$$\sin{75^{\circ}}=\dfrac{h}{x},$$
$$h=x\, \sin{75^{\circ}}=50\cdot\dfrac{\sqrt{3}}{\sqrt{2}}\cdot\dfrac{\sqrt{2}}{4}(\sqrt{3}+1)=\dfrac{75}{2}+\dfrac{25}{2}\sqrt{3}$$
puisque
$$\begin{array}{rcl} \sin{75^{\circ}}=\sin{(45^{\circ}+30^{\circ})}&=&\sin{45^{\circ}}\cos{30^{\circ}}+\sin{30^{\circ}}\cos{45^{\circ}}\\ &=&\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\\ &=&\dfrac{\sqrt{2}}{4}(\sqrt{3}+1). \end{array}$$
Finalement, $d=h-10=\dfrac{75}{2}+\dfrac{25}{2}\sqrt{3}-10=\dfrac{25}{2}\sqrt{3}+\dfrac{55}{2}$ mètres.
-
A partir d'un point $A$ situé $8$ mètres au-dessus du sol, l'angle d'élévation du sommet d'un bâtiment est de $30^{\circ}$ et l'angle de dépression de la base du bâtiment est de $15^{\circ}$. Calculez la hauteur du bâtiment.
On peut représenter la situation par le shéma suivant
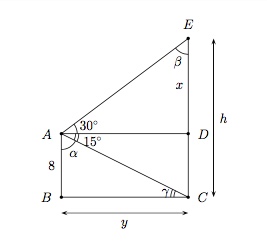
$\bullet\, $ calculez les angles
$\bullet\, $ déterminez $y$ dans le triangle rectangle $ABC$
$\bullet\, $ cherchez $x$ dans le triangle rectangle $ADE$
$\bullet\, $ déduisez-en $h$
On peut représenter la situation par le shéma suivant

Commençons par rechercher les angles : $\alpha=90^{\circ}-15^{\circ}=75^{\circ}$ (angles complémentaires), $\beta=90^{\circ}-30^{\circ}=60^{\circ}$ (somme des angles intérieurs d'un triangle) et $\gamma=15^{\circ}$ (angles alternes-internes).
Déterminons $y$ dans le triangle rectangle $ABC$. On a $\mbox{ tg }\alpha=\frac{\mbox{opposé}}{\mbox{adjacent}}$ et donc $\mbox{ tg }75^{\circ}=\frac{y}{8}$. On en déduit $y=8\, \mbox{ tg }75^{\circ}$.
Déterminons $x$ dans le triangle rectangle $ADE$. On a $\mbox{ tg }30^{\circ}=\frac{x}{y}$. On en déduit $x=y\, \mbox{ tg }30^{\circ}$ et donc $x=8\, \mbox{ tg }75^{\circ}\, \mbox{ tg }30^{\circ}$.
Finalement, en utilisant les formules d'addition, on a
$$\mbox{ tg }75^{\circ}=\mbox{ tg }(45^{\circ}+30^{\circ})=\frac{\mbox{ tg }45^{\circ}+\mbox{ tg }30^{\circ}}{1-\mbox{ tg }45^{\circ}\, \mbox{ tg }30^{\circ}}=\frac{1+\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}=\frac{3+\sqrt{3}}{3-\sqrt{3}}.$$
On en déduit que $x=8\cdot\frac{3+\sqrt{3}}{3-\sqrt{3}}\cdot\frac{\sqrt{3}}{3}=17,24$ et donc la hauteur du bâtiment est $h=x+8=17,24+8=25,24$ mètres.