Exercices résolus
Voici quelques exemples d'exercices résolus en détails.
-
Lorsque l'angle d'élévation du soleil est de $64^{\circ}$, un poteau téléphonique qui penche d'un angle de $9^\circ$ par rapport à une ligne formée par le pied du poteau et le soleil projette une ombre de 6,3 mètres sur le sol. Déterminez la hauteur du poteau.
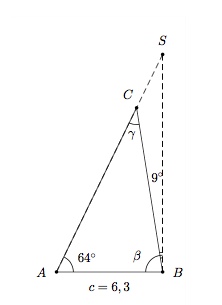
Le triangle $ABC$ représente les faits. On a $\alpha= 64^\circ$, $\beta =90^\circ - 9^\circ = 81^\circ$ et $\gamma = 180^\circ- 64^\circ-81^\circ = 35^\circ$.
Pour calculer la hauteur du poteau, c'est-à-dire le côté $a=BC$ du triangle $ABC$, on utilise la Règle des sinus :
$$\frac{\sin \alpha}{a}=\frac{\sin \gamma}{c},$$
c'est-à-dire
$$\frac{\sin 64^\circ}{a}=\frac{\sin 35^\circ}{6,3},$$
d'où $ a=6,3\cdot \dfrac{\sin 64^\circ}{\sin 35^\circ}=9,87$ mètres.
-
Sur le flanc d'une montagne se trouve une tour. Un observateur se trouvant à 320 mètres de la tour la voit sous un angle de $6^{\circ}$. Il monte alors dans la direction de la tour et, après avoir parcouru 220 mètres, il la voit sous un angle de $13^{\circ}$. Déterminez la hauteur de cette tour.
On peut représenter la situation par le shéma suivant
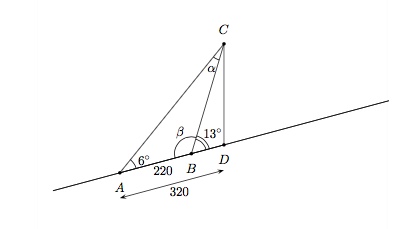
On déduit des données que l'angle $\beta=180^{\circ}-13^{\circ}=167^{\circ}$, donc l'angle $\alpha=180^{\circ}-167^{\circ}-6^{\circ}=7^{\circ}$.
On déduit la longueur du côté $AC$ de la Règle des sinus :
$$\dfrac{220}{\sin{7^{\circ}}}=\dfrac{\vert AC\vert}{\sin{167^{\circ}}}$$
et donc $\vert AC\vert=220\cdot \dfrac{\sin{167^{\circ}}}{\sin{7^{\circ}}}=406,1$ mètres.
Finalement, par la Règle des cosinus, on obtient
$$ \begin{array}{rcl} h^2=\vert CD\vert^2 &= &\vert AD\vert^2+\vert AC\vert^2-2\vert AD\vert\, \vert AC\vert\, \cos{6^{\circ}} \\ & = &320^2+\left( 220\cdot \dfrac{\sin{167^{\circ}}}{\sin{7^{\circ}}}\right)^2 -2\cdot 320\cdot \left( 220\cdot \dfrac{\sin{167^{\circ}}}{\sin{7^{\circ}}}\right) \cdot\cos{6^{\circ}} \\ & = &8836,99 \end{array} $$
et donc $h=\sqrt{h^2}\approx 94$ mètres.
-
Deux villes $A$ et $B$ sont reliées par une route rectiligne directe. Des travaux sur cette route obligent l'automobiliste à effectuer un détournement par la ville $C$ située à $4\sqrt{3}$ km de la route directe. Calculez le nombre de kilomètres supplémentaires que devra parcourir l'automobiliste à cause de cette déviation, sachant que les routes $AC$ et $CB$ sont rectilignes, que les routes $AC$ et $AB$ forment un angle de $60^{\circ}$ et que la route $AB$ mesure 50 km.
On peut représenter la situation par le shéma suivant
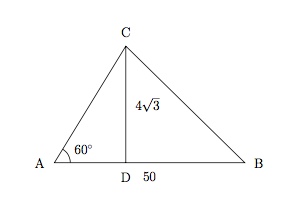
Règle des sinus dans $ACD$ : $\dfrac{|AC|}{\sin(90^{\circ})}=\dfrac{4\sqrt{3}}{\sin{60^{\circ}}}$, c'est-à-dire $|AC|=8$.
Règle des cosinus dans $ABC$ : $|BC|^2=|AB|^2+|AC|^2-2|AB|\, |AC|\, \cos{60^{\circ}}=2164$. On en déduit que $|BC|=\sqrt{2164}$.
La déviation est donc de $|AC|+|BC|=8+\sqrt{2164}$ km.
Il y aura donc $8+\sqrt{2164}-50=\sqrt{2164}-42$ km supplémentaires.