Questions de théorie
Ces questions sont destinées à vous faire revoir la théorie de ce chapitre.
Enoncez la Règle des sinus.
L'énoncé se trouve dans le syllabus, chapitre 4, section 2.
Règle des sinus : Dans tout triangle, les longueurs des côtés sont proportionnelles aux sinus des angles opposés, c'est-à-dire si $a$, $b$ et $c$ sont les longueurs des côtés d'un triangle et $\alpha$, $\beta$ et $\gamma$ sont les angles opposés respectivement à ces côtés, on a
$$\frac{\sin \alpha}{a}=\frac{\sin \beta}{b}=\frac{\sin \gamma}{c}.$$
Démontrez que la Règle des sinus.
La démonstrastion se trouve dans le syllabus, chapitre 4, section 2.
Pour un triangle quelconque $ABC$, plaçons $A$ en l'origine et $B$ sur la partie positive de l'axe $OX$. Le point $C$ est donc au-dessus de l'axe $OX$. Traçons la hauteur $h$ perpendiculaire à $c$. Elle coupe le côté $c$ au point $D$.
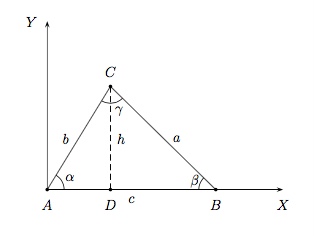
Si on pose que la distance de $C$ à $D$ vaut $h$, alors l'ordonnée de $C$ est $h$. Par la définition des nombres trigonométriques, on a
$$h = b.\sin \alpha.$$
De même, en regardant le triangle $BDC$, on a
$$h = a.\sin \beta,$$
d'où,
$$\frac{\sin \alpha}{a}=\frac{\sin \beta}{b}.$$
Par un argument similaire (en plaçant $A$ en l'origine et $C$ sur la partie positive de l'axe $OX$), on obtient que
$$\frac{\sin \alpha}{a}=\frac{\sin \gamma}{c}.$$
Démontrez la Règle des sinus en utilisant le rayon du cercle circonscrit au triangle.
Déplacez le sommet $A$ le long du cercle circonscrit sans changer $a$ ni $\alpha$.
On considère le cercle circonscrit au triangle
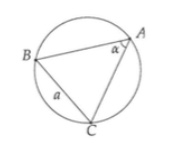
On peut bouger le sommet $A$ sans changer $a$ et $\alpha$. On le place de manière à ce que $\widehat{BCA}$ soit un angle droit. Dans ce cas, $BA$ est un diamètre de longueur $2R$ et on a $$\sin{\alpha}=\dfrac{a}{2R}$$ ou encore $$\dfrac{\sin{\alpha}}{a}=\dfrac{1}{2R}.$$
Par le même raisonnement avec les côtés $b$ et $c$, on obtient $$\dfrac{\sin{\beta}}{b}=\dfrac{1}{2R}$$ et $$\dfrac{\sin{\gamma}}{c}=\dfrac{1}{2R}.$$
Finalement, on a $$\dfrac{\sin{\alpha}}{a}=\dfrac{\sin{\beta}}{b}=\dfrac{\sin{\gamma}}{c}=\dfrac{1}{2R}.$$
Enoncez la Règle des cosinus. Pourquoi ce résultat généralise-t-il le Théorème de Pythagore ?
L'énoncé se trouve dans le syllabus, chapitre 4, section 2.
Règle des cosinus : Dans tout triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés diminuée du double produit des longueurs de ces deux côtés par le cosinus de l'angle compris entre ces côtés, c'est-à-dire si $a$, $b$ et $c$ sont les longueurs des côtés d'un triangle et $\alpha$, $\beta$ et $\gamma$ sont les angles opposés respectivement à ces côtés, on a
$$ \begin{array}{l} a^2=b^2+c^2-2bc\cos{\alpha} \\ b^2=a^2+c^2-2ac\cos{\beta} \\ c^2=a^2+b^2-2ab\cos{\gamma} \end{array} $$
Ce résultat est une généralisation du Théorème de Pythagore. En effet, par exemple dans la dernière formule ci-dessus, si le triangle est rectangle en $C$ alors $c$ est l'hypoténuse du triangle, $\gamma=90^{\circ}$ et on retrouve la formule de Pythagore $c^2=a^2+b^2$.
Démontrez la Règle des cosinus.
La démonstrastion se trouve dans le syllabus, chapitre 4, section 2.
Pour un triangle quelconque $ABC$, plaçons $A$ en l'origine et $B$ sur la partie positive de l'axe $OX$. Le point $C$ est donc au-dessus de l'axe $OX$. Traçons la hauteur $h$ perpendiculaire à $c$. Elle coupe le côté $c$ au point $D$.

Dans le triangle rectangle $BCD$, on a
$$ \begin{array}{rl} \vert BC\vert^2 & =\vert BD\vert^2+\vert DC\vert^2 \\ & =(\vert AB\vert-\vert DA\vert)^2+\vert DC\vert^2 \\ & =\vert AB\vert^2+\vert DA\vert^2-2\vert AB\vert\cdot\vert DA\vert+\vert DC\vert^2 \\ & =\vert AB\vert^2+(\vert DA\vert^2+\vert DC\vert^2)-2\vert AB\vert\cdot \vert DA\vert \end{array} $$
Dans le triangle rectangle $ACD$, on a $$\vert DA\vert^2+\vert DC\vert^2=\vert AC\vert^2$$ et aussi $$\vert DA\vert=\vert AC\vert\cos{\alpha}.$$
On en déduit $$\vert BC\vert^2=\vert AB\vert^2+\vert AC\vert^2-2 \vert AB\vert\cdot\vert AC\vert\cos{\alpha}$$ ou encore $$a^2=c^2+b^2-2bc\cos{\alpha}.$$
Les deux autres égalités s'obtiennent de façon analogue.
Enoncez le Théorème de la médiane.
L'énoncé se trouve dans le syllabus, chapitre 4, section 2.
Théorème de la médiane : La somme des carrés des longueurs de deux côtés d'un triangle est égale à deux fois le carré de la longueur de la médiane relative au troisième côté plus deux fois le carré de la moitié de la longueur du troisième côté.
Démontrez le Théorème de la médiane.
La démonstrastion se trouve dans le syllabus, chapitre 4, section 2.
On considère le triangle
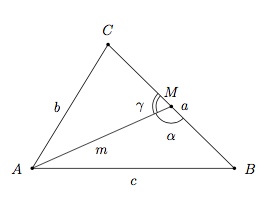
On a par la règle des cosinus dans le triangle $ACM$
$$b^2=m^2+\left(\dfrac{a}{2}\right)^2-2m\dfrac{a}{2}\cos{\gamma}$$
et par la règle des cosinus dans le triangle $AMB$
$$c^2=m^2+\left(\dfrac{a}{2}\right)^2-2m\dfrac{a}{2}\cos{\alpha}.$$
On en déduit que
$$ \begin{array}{l} b^2+c^2=2m^2+2\left(\dfrac{a}{2}\right)^2-ma(\cos{\gamma}+\cos{\alpha}) \\ b^2+c^2=2m^2+2\left(\dfrac{a}{2}\right)^2-ma(\cos{\gamma}+\cos{(\pi-\gamma)}) \\ b^2+c^2=2m^2+2\left(\dfrac{a}{2}\right)^2-ma(\cos{\gamma}-\cos{\gamma}) \end{array} $$
et donc
$$b^2+c^2=2m^2+2\left(\dfrac{a}{2}\right)^2.$$
Calculez la longueur des médianes en fonction de la longueur des côtés d'un triangle.
Utilisez le Théorème de la médiane dans le triangle $ABC$ puis déduisez-en la longueur $|AM|$.

On déduit du Théorème de la médiane que
$$|AC|^2+|AB|^2=2|AM|^2+2\left(\dfrac{|BC|}{2}\right)^2.$$
On en tire
$$2|AM|^2=|AC|^2+|AB|^2-\dfrac{|BC|^2}{2},$$
$$4|AM|^2=2|AB|^2+2|AC|^2-|BC|^2,$$
$$|AM|=\dfrac{1}{2}\sqrt{2|AB|^2+2|AC|^2-|BC|^2}.$$
Donc $|AM|=\dfrac{1}{2}\sqrt{2c^2+2b^2-a^2}$.