Exercices pour s’entraîner

La particularité du papier au format $A_n$ est qu'en coupant sa longueur en deux parties égales on retrouve deux rectangles égaux de format $A_{n+1}$.

Si le rectangle initial a pour longueur $L$ et pour largeur $l$, après un découpage on obtient deux rectangles de longueur $l$ et largeur $\frac{L}{2}$. Pour qu'ils aient la même forme que le rectangle initial, il faut que $$ k=\dfrac{L}{l}=\dfrac{l}{\frac{L}{2}} $$ ou encore que $k=\frac{2}{k}$, c'est-à-dire $k^2=2$ et donc $k=\sqrt{2}$.

Comme le format $A_0$ est choisit pour avoir une surface d'un mètre carré, on en déduit que les dimensions du papier de format $A_4$ vérifient le système $$ \left\{ \begin{array}{l} L\cdot l=\frac{1}{16}\\ \frac{L}{l}=\sqrt{2} \end{array} \right. $$ et $$ L\cdot l=\dfrac{1}{16} $$ $$ \sqrt{2}\, l^2=\dfrac{1}{16} $$ $$ l^2=\dfrac{1}{2^4}\cdot\dfrac{1}{2^{1/2}}=\dfrac{1}{2^{9/2}}=2^{-9/2} $$ $$ l=\left(2^{-9/2}\right)^{1/2}=2^{-9/4} $$ et donc $L=\sqrt{2}\, l=2^{1/2}\cdot 2^{-9/4}=2^{-7/4}$.

Les dimensions du format $A_4$ sont donc $L=2^{-7/4}\simeq 0,2973$ mètres et $l=2^{-9/4}\simeq 0,21$ mètres.

On a $r=50\mbox{ cm}$ et $\theta=60^{\circ}=\frac{\pi}{3}\mbox{ radians}$.

On en déduit que $L=r\theta=50\cdot\frac{\pi}{3}=52,359\mbox{ cm}$.

Soit $x$= base et $y$= hauteur du triangle. Son aire vaut $\dfrac{xy}{2}$.

Si base = $\dfrac{x}{2}$ et hauteur = $3y$ alors l'aire vaut $\dfrac{3xy}{4}=\dfrac{3}{2}\cdot\dfrac{xy}{2}$.

Donc l'aire est multipliée par $\dfrac{3}{2}$.

Soit $x$= diamètre du disque. Son rayon vaut $\left(\dfrac{x}{2}\right)$ et son aire vaut $\pi \left(\dfrac{x}{2}\right)^2=\dfrac{\pi\, x^2}{4}$.

Si diamètre = $2x$ alors le rayon vaut $x$ et l'aire vaut $\pi\, x^2$.

Donc l'aire est multipliée par $4$.

Soit $E$ la projection orthogonale de $B$ sur $DC$.

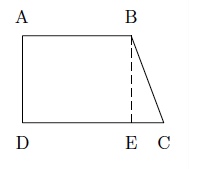
On a $$ \mbox{tg }60^{\circ}=\dfrac{|BE|}{|EC|}\mbox{ d'où }|EC|=\dfrac{|BE|}{\mbox{tg }60^{\circ}}=\dfrac{4}{\sqrt{3}}=\dfrac{4\sqrt{3}}{3}. $$De plus, par Pythagore, on obtient $$ |BC|^2=|BE|^2+|EC|^2=16+\dfrac{16}{3}=\dfrac{64}{3}\mbox{ et donc }|BC|=\dfrac{8\sqrt{3}}{3}. $$ Le périmètre du trapèze vaut donc $$ P=5+4+5+\dfrac{4\sqrt{3}}{3}+\dfrac{8\sqrt{3}}{3}=14+4\sqrt{3}\mbox{ cm} $$ et son aire vaut $$ A=\left(5+5+\dfrac{4\sqrt{3}}{3}\right)\cdot 4\cdot\dfrac{1}{2}=20+\dfrac{8\sqrt{3}}{3}\mbox{ cm}^2. $$

Par Pythagore dans le triangle $GEF$, on a $|GE|=\sqrt{1+1}=\sqrt{2}$ et donc $|BE|=|BG|+|GE|=1+\sqrt{2}$.

Par Thalès, on a $$ \dfrac{|BG|}{|BE|}=\dfrac{|CG|}{|DE|}, \mbox{ c'est-à-dire }\dfrac{1}{1+\sqrt{2}}=\dfrac{1}{|DE|} $$ et donc $|DE|=1+\sqrt{2}$.

Par Thalès, on a aussi $$ \dfrac{|CF|}{|AF|}=\dfrac{|DE|}{|AE|},\mbox{ c'est-à-dire }\dfrac{2}{|AF|}=\dfrac{1+\sqrt{2}}{|AF|+1} $$ d'où $|AF|(\sqrt{2}-1)=2$ et $|AF|=2\sqrt{2}+2$.

On en déduit que $|AE|=|AF|+|FE|=2\sqrt{2}+3$.

L'aire du triangle $AED$ est $\dfrac{|AE|\cdot |DE|}{2}=\dfrac{5\sqrt{2}+7}{2}$.

L'aire du trapèze $CDEG$ est $\dfrac{(|DE|+|CG|)\cdot |EF|}{2}=\dfrac{2+\sqrt{2}}{2}$.

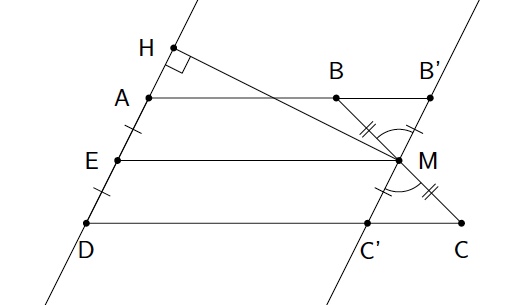
Soit $M$ le milieu du segment $BC$ et $MH$ la perpendiculaire à $AD$ passant par $M$.  Il faut voir que l'aire de $ABCD$ est donnée par $|AD|\cdot |MH|$.

Traçons par $M$ la parallèle à $AD$ qui rencontre $AB$ en $B'$ et $CD$ en $C'$.  On en déduit que $AB'C'D$ est un parallélogramme.

Traçons par $M$ la parallèle aux bases. Elle coupe $AD$ en $E$.  Puisque $M$ est le milieu de $BC$, $E$ est le milieu de $AD$ et on en déduit que $M$ est le milieu de $B'C'$.

Puisque

$\bullet\, |BM|=|MC|$

$\bullet\, |B'M|=|MC'|$

$\bullet\, \widehat{M_1}=\widehat{M_2}$ car angles opposés par le sommet

on en déduit que les triangles $MBB'$ et $MCC'$ sont égaux.

Donc aire ($ABCD$)=aire($AB'C'D$)=$|AD|\cdot |MH|$.