Questions de théorie
Ces questions sont destinées à vous faire revoir la théorie de ce chapitre.
Définissez le développement d'un solide.
La définition se trouve dans le syllabus au chapitre 6, section 3.
Le développement d'un solide est la figure plane obtenue par la mise à plat de sa surface. Le développement est une figure plane telle que si on la plie aux endroits appropriés, on obtient un solide en collant entre eux les bords libres.
Donnez le développement d'un tétraèdre, d'un octaèdre, d'un icosaèdre, d'un cube et d'un dodécaèdre. Précisez le nombre de polygones de chaque type apparaissant dans le développement.
Le développement d'un solide est la figure plane obtenue par la mise à plat de sa surface. Le développement est une figure plane telle que si on la plie aux endroits appropriés, on obtient un solide en collant entre eux les bords libres.
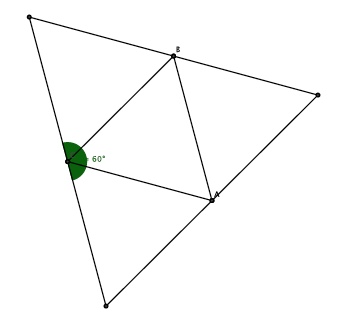
Développement du tétraèdre : 4 triangles équilatéraux
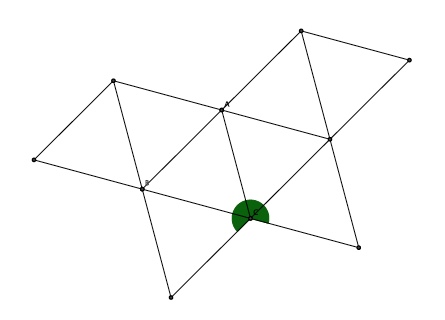
Développement de l'octaèdre : 8 triangles équilatéraux
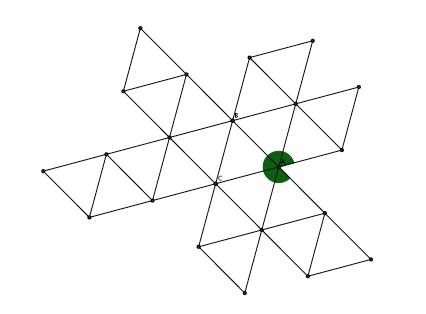
Développement de l'icosaèdre : 20 triangles équilatéraux
Développement du cube : 6 carrés
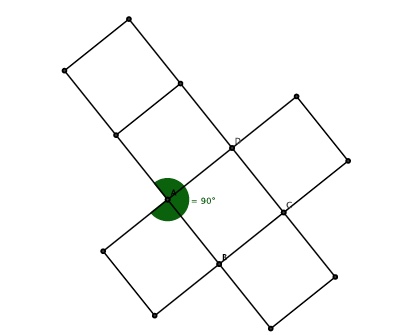
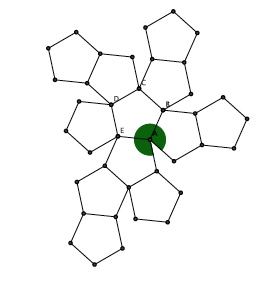
Développement du dodécaèdre : 12 pentagones
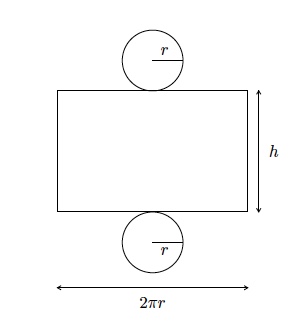
Donnez le développement du cylindre circulaire droit de hauteur $h$ et rayon $r$.
Le développement se trouve dans le syllabus au chapitre 6, section 3.
Le développement d'un cylindre circulaire droit de rayon $r$ et de hauteur $h$ est constitué de deux disques isométriques de rayon $r$ et d'un rectangle de hauteur $h$ et de largeur $2\pi r$.
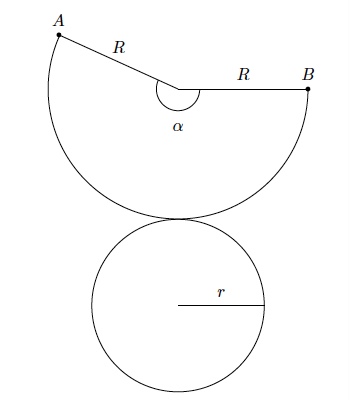
Donnez le développement du cône circulaire droit de rayon $r$ et génératrice $R$.
Le développement se trouve dans le syllabus au chapitre 6, section 3.
Le développement d'un cône circulaire droit de rayon $r$ et de génératrice $R$ est constitué d'un disque de rayon $r$ et d'un secteur circulaire de rayon $R$ et d'angle $\alpha=\frac{360r}{R}$.