Questions de théorie

On appelle polyèdre un solide limité de toutes parts par des portions de plans.   Les faces d'un polyèdre sont les polygones plans qui composent la surface du polyèdre. Les arêtes d'un polyèdre sont les côtés des polygones qui forment les faces du polyèdre. Les sommets du polyèdre sont les extrémités des arêtes.

Un polyèdre est convexe si tout segment ayant ses extrémités dans le polyèdre y est inclus tout entier.

Un prisme est un polyèdre ayant pour base deux polygones égaux et parallèles et dont les faces latérales sont des parallélogrammes. Les deux polygones translatés sont les bases du prisme et les parallélogrammes sont appelés faces latérales. La hauteur d'un prisme est la distance entre les plans des bases. C'est la hauteur de la perpendiculaire commune aux deux bases.

Un prisme est droit lorsque les arêtes latérales sont perpendiculaires à la base, sinon on dit qu'il est oblique.

Une pyramide est un polyèdre dont la surface est constituée d'un polygone à $n$ côtés appelé base et de $n$ triangles ayant chacun un côté commun avec la base et ayant tous un point commun n'appartenant pas au plan de la base. Le sommet de la pyramide est le point commun aux $n$ triangles. Sa hauteur est la longueur du segment de droite mené du sommet perpendiculairement à la base et limité par le sommet et la base.

Un polyèdre régulier est un polyèdre convexe constitué de polygones réguliers isométriques en même nombre autour de chaque sommet.

Un polyèdre régulier est inscriptible dans une sphère.

Tout polyèdre régulier admet une sphère inscrite, c'est-à-dire une sphère qui lui est intérieure et tangente à chaque face.

Il existe cinq polyèdres réguliers, appelés aussi solides de Platon. En effet, un polyèdre régulier doit avoir le même nombre de polygones réguliers en chacun de ses sommets. Ce nombre est évidemment au minimum de 3. Le maximum dépendra de l'angle du polygone régulier : si la somme des angles au sommet atteint ou dépasse 360$^{\circ}$, nous obtenons un plan ou une superposition des faces.

Si nous plaçons 3 triangles équilatéraux en chaque sommet du polyèdre régulier, nous obtenons le tétraèdre régulier.

Si nous plaçons 4 triangles équilatéraux en chaque sommet du polyèdre régulier, nous obtenons l'octaèdre régulier.

Si nous plaçons 5 triangles équilatéraux en chaque sommet du polyèdre régulier, nous obtenons l'icosaèdre régulier.

Si nous plaçons 3 carrés en chaque sommet du polyèdre régulier, nous obtenons le cube.

Si nous plaçons 3 pentagones réguliers en chaque sommet du polyèdre régulier, nous obtenons le dodécaèdre.

\begin{array}{|l|l|c|c|} \hline \textbf{Polyèdre} & \textbf{Faces} & \textbf{Sommets} & \textbf{Arêtes} \\ \hline tétraèdre & 4\, triangles & 4 & 6 \\ cube & 6\, carrés & 8 & 12 \\ octaèdre & 8\, triangles & 6 & 12 \\ dodécaèdre & 12\, pentagones & 20 & 30 \\ icosaèdre & 20\, triangles & 12 & 30 \\ \hline \end{array}

Dans tout polyèdre convexe, régulier ou non, on a $$ S+F=A+2, $$ où $S$, $F$ et $A$ sont respectivement le nombre de sommets, de faces et d'arêtes du polyèdre.

On commence par enlever une face et on aplatit le polyèdre pour obtenir un graphe plan appelé diagramme de Schlegel du polyèdre.

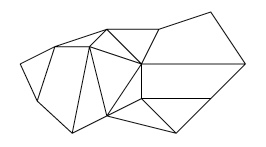
On a $S'=S$, $F'=F-1$ et $A'=A$, où $S'$, $F'$ et $A'$ sont respectivement le nombre de sommets, de faces et d'arêtes du graphe plan.

Pour chaque face non triangulaire, on ajoute une arête reliant deux sommets non appariés. On répète l'opération tant qu'il reste des faces non triangulaires.

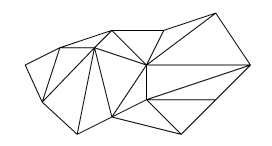
A chaque fois, on augmente le nombre d'arêtes de $1$ et le nombre de faces de $1$ : $$ S'+(F'+1)-(A'+1)=S'+F'+1-A'-1=S'+F'-A'. $$ La quantité $S'+F'-A'$ n'est donc pas modifiée.

On alterne les deux opérations suivantes :

$\rightsquigarrow$ supprimer les triangles dont une seul arête est frontière.

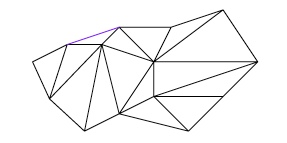
A chaque fois, on diminue le nombre d'arêtes et de faces de $1$ : $$ S'+(F'-1')-(A'-1)=S'+F'-1-A'+1=S'+F'-A'. $$ La quantité $S'+F'-A'$ n'est donc pas modifiée.

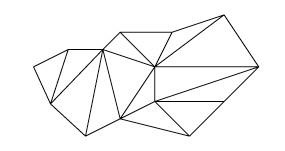
$\rightsquigarrow$ supprimer les triangles dont deux arêtes sont frontière.

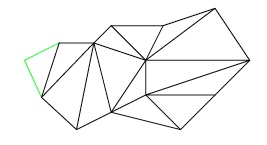
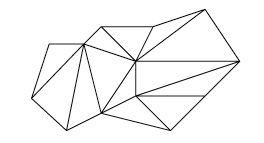
A chaque fois, on diminue le nombre d'arêtes de $2$ et le nombre de faces et de sommets de $1$ : $$ (S'-1)+(F'-1)-(A'-2)=S'-1+F'-1-A'+2=S'+F'-A'. $$ La quantité $S'+F'-A'$ n'est donc pas modifiée.

On répète le processus jusqu'à ce qu'il ne reste qu'un seul triangle.

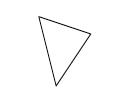
Pour un triangle, on a $S'=3$, $F'=1$ et $A'=3$ donc $$ S'+F'-A'=3+1-3=1. $$ Puisque la quantité $S'+F'-A'$ n'est pas modifiée par les opérations ci-dessus, on a aussi $S'+F'-A'=1$ pour le graphe plan de départ.

Si on rajoute la face enlevée à la première étape, on obtient pour le polyèdre $$ S+F-A=S'+F'+1-A'=S'+F'-A'+1=2. $$

Les solides d'Archimède sont des polyèdres convexes dont les faces sont composées d'au moins deux sortes de polygones réguliers convexes, dont les arêtes ont toutes la même longueur et tels qu'en chaque sommet il y a la même configuration.

On peut inscrire les solides d'Archimède dans une sphère, c'est-à-dire qu'il existe une sphère contenant tous les sommets.

Il y a 13 solides d'Archimède.