Exercices pour s’entraîner
Entraînez-vous à résoudre les exercices suivants.
-
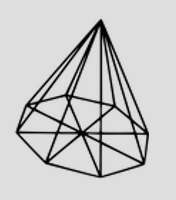
Déterminez le volume du solide ci-dessous de hauteur $8$ cm si la base est formée de triangles équilatéraux de $3$ cm de côté.
Le volume d'une pyramide est donné par $V=\frac{Bh}{3}$ où $B$ est l'aire de la base et $h$ est la hauteur de la pyramide.
La base est formée de $8$ triangles équilatéraux de $3$ cm de côté. On déduit du Théorème de Pythagore que la hauteur d'un de ces triangles vaut $\frac{3\sqrt{3}}{2}$ cm. La surface d'un de ces triangles vaut donc $\frac{9\sqrt{3}}{4}$ cm$^2$ et la surface de la base vaut $B=8\cdot \frac{9\sqrt{3}}{4}=18\sqrt{3}$ cm$^2$.
Le volume de la pyramide vaut donc $V=\frac{Bh}{3}=\frac{18\sqrt{3}\cdot 8}{3}=48\sqrt{3}$ cm$^3$.
-
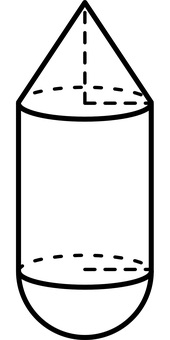
Déterminez le volume du solide ci-dessous constitué d'une demi-sphère de rayon $3$ cm, d'un cône de rayon $3$ cm et de hauteur $4$ cm et d'un cylindre de rayon $3$ cm et de hauteur $6$ cm.
Le volume d'une sphère de rayon $r$ est donné par $\frac{4}{3}\, \pi\, r^3$.
Le volume d'un cône de rayon $r$ et hauteur $h$ est donné par $\frac{\pi\, r^2\, h}{3}$.
Le volume d'un cylindre de rayon $r$ et hauteur $h$ est donné par $\pi\, r^2\, h$.
Le volume de la demi-sphère de rayon $3$ vaut $\frac{108\, \pi}{6}=18\, \pi$ cm$^3$.
Le volume du cylindre de rayon $3$ et hauteur $6$ vaut $54\, \pi$ cm$^3$.
Le volume du cône de rayon $3$ et hauteur $4$ vaut $\frac{36\, \pi}{3}=12\, \pi$ cm$^3$.
Le volume total du solide est donc $$V=18\, \pi+54\, \pi+12\, \pi=84\, \pi\mbox{ cm}^3.$$
-
Déterminez le volume du solide ci-dessous.

Un tétraèdre régulier est constitué de 4 triangles équilatéraux.
Le volume d'un tétraèdre régulier est donné par $V=\frac{Bh}{3}$ où $B$ est l'aire de la base et $h$ est la hauteur du tétraèdre.
La base est formée d'un triangle équilatéral de $3$ cm de côté. On déduit du Théorème de Pythagore que la hauteur de ce triangle vaut $\frac{3\sqrt{3}}{2}$ cm. La surface de la base vaut donc $B=\frac{9\sqrt{3}}{4}$ cm$^2$.
La hauteur du tétraèdre relie le sommet à un point de la base situé au $\frac{2}{3}$ d'un des sommets de la base. On déduit du Théorème de Pythagore que la hauteur du tétraèdre vaut $h=\sqrt{6}$ cm.
Finalement, le volume du tétraèdre est donné par $$V=\frac{Bh}{3}=\frac{9\sqrt{3}}{4}\cdot\frac{\sqrt{6}}{3}=\frac{9\sqrt{2}}{4}\mbox{ cm}^3.$$
-
Que faire pour doubler le volume d'un cône circulaire ?
Le volume d'un cône de rayon $r$ et hauteur $h$ est donné par $\frac{\pi\, r^2\, h}{3}$.
Volume = $V=\frac{\pi r^2h}{3}$.
Si $V'=2V$ alors $\dfrac{\pi r'^2h'}{3}=\dfrac{2\pi r^2h}{3}$.
Donc $r'=\sqrt{2}r$ et $h'=h$ ou $r'=r$ et $h'=2h$.
-
On double le rayon d'un cône circulaire et on divise par trois sa hauteur. Que devient son volume ?
Le volume d'un cône de rayon $r$ et hauteur $h$ est donné par $\frac{\pi\, r^2\, h}{3}$.
Soit $r$= rayon et $h$= hauteur du cône. Son volume vaut $V=\dfrac{\pi r^2h}{3}$.
Si rayon = $2r$ et hauteur = $\frac{h}{3}$ alors le volume vaut $$\dfrac{\pi}{3}(2r)^2\cdot\dfrac{h}{3}=\dfrac{\pi}{3}\cdot 4r^2\cdot\dfrac{h}{3}=\dfrac{4}{3}\left(\dfrac{\pi r^2h}{3}\right)=\dfrac{4}{3}V.$$
Donc le volume est multiplié par $\frac{4}{3}$.
-
Calculez le volume d'un prisme droit régulier à base carrée, sachant qu'il est inscrit dans un cylindre de révolution de hauteur $0,75$ m et dont la circonférence de base a une longueur de $0,95$ m.
Le volume d'un prisme de base $B$ et hauteur $h$ est donné par $Bh$.
Rayon du cylindre : $2\pi r=0,95\mbox{ m}$ d'où $r=\dfrac{0,95}{2\pi}\mbox{ m}$.
Soit $x$ la longueur de l'arête du prisme.
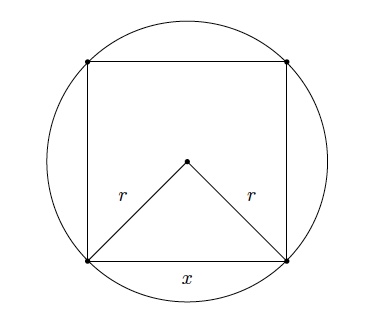
On a $x^2=r^2+r^2$ d'où $x=\sqrt{2}\, r$.
Volume du prisme : $$V=x^2\, h=2r^2\, h=2\cdot\left(\dfrac{0,95}{2\pi}\right)^2\cdot 0,75=0,0343\mbox{ m}^3=34,3\mbox{ dm}^3.$$