Exercices résolus
Voici quelques exemples d'exercices résolus en détails.
-
Déterminez le volume du solide ci-dessous.
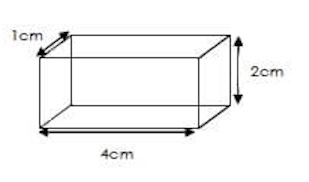
Le volume d'un parallélipipède rectangle de dimensions $L$, $l$ et $h$ est donné par $V=Llh$. Ici le volume est $8$ cm$^3$.
-
Que faire pour doubler le volume d'un parallélipipède rectangle ? Que devient son aire latérale ?
Le volume d'un parallélipipède rectangle de dimensions $L$, $l$ et $h$ est donné par $V=Llh$.
Pour doubler le volume on peut par exemple multiplier $L$ ou $l$ ou $h$ par deux.
Si $h'=2h$ alors $V'=Llh'=2Llh=2V$.
\begin{array}{rcl} \mbox{Aire latérale }A' &=&2(Ll+lh'+Lh')=2(Ll+2lh+2Lh)\\ &=&2Lh+4lh+4Lh=A+2lh+2Lh. \end{array}
-
Un cône est engendré par un triangle rectangle dont l'angle aigu, au sommet du cône, vaut 30 degrés. Le rayon de la base du cône a 17 cm. Déterminez la surface totale du cône et son volume.
Hauteur du cône : $\mbox{tg }{30^{\circ}}=\frac{17}{h}$ d'où $$h=\dfrac{17}{\mbox{tg }{30^{\circ}}}=\dfrac{17}{\frac{1}{\sqrt{3}}}=17\sqrt{3}.$$
On en déduit la surface du cône : $$S=\pi r\sqrt{r^2+h^2}+\pi r^2=\pi\cdot 17\sqrt{17^2+17^2\cdot 3}+\pi\cdot 17^2=2723,76\mbox{ cm}^2.$$
Et son volume : $$V=\dfrac{\pi r^2 h}{3}=\dfrac{\pi}{3}\cdot 17^2\cdot 17\sqrt{3}=8911,19\mbox{ cm}^3.$$