Questions de théorie

Le parallélipipède rectangle dont la base est un rectangle de longueur $L$ et de largeur $l$ et dont la hauteur est $h$ a pour volume le nombre $V=Llh$.

Le cylindre circulaire droit dont la base est un disque de rayon $r$ et dont la hauteur est $h$ a pour volume le nombre $V=\pi\, r^2\, h$.

Principe de Cavalieri : Soit deux solides compris entre deux plans parallèles. Supposons que chaque plan parallèle aux premiers coupe les deux solides en des surfaces de même aire. Alors, dans ces conditions, les deux solides ont même volume.

Le Principe de Cavalieri permet de déterminer le volume de n'importe quel prisme ou cylindre en le comparant "tranche par tranche" avec un solide de volume connu.

On va comparer le parallélipipède "tranche par tranche" avec un parallélipipède rectangle de même base et même hauteur, ce qui revient à les couper par une infinité de plans parallèles à leur base. En coupant à toute hauteur on obtient des sections de même aire et on conclut du Principe de Cavalieri que ces deux solides ont même volume.

Le parallélipipède dont la base vaut $B$ et la hauteur $h$ a pour volume le nombre $V=Bh$.

On va comparer le prisme "tranche par tranche" avec un parallélipipède dont l'aire de la base et la hauteur sont les mêmes, ce qui revient à les couper par une infinité de plans parallèles à leur base. En coupant à toute hauteur on obtient des sections de même aire et on conclut du Principe de Cavalieri que ces deux solides ont même volume.

Le prisme dont la base vaut $B$ et la hauteur $h$ a pour volume le nombre $V=Bh$.

On va comparer le cylindre "tranche par tranche" avec un cylindre circulaire droit de même base et même hauteur, ce qui revient à les couper par une infinité de plans parallèles à leur base. En coupant à toute hauteur on obtient des sections de même aire et on conclut du Principe de Cavalieri que ces deux solides ont même volume.

Le cylindre dont la base vaut $B$ et la hauteur $h$ a pour volume le nombre $V=Bh$.

Deux pyramides à bases triangulaires de même hauteur et dont l'aire de la base est la même ont même volume.

En effet, si on les coupe à distance $m$ du sommet $S$ par un plan parallèle à la base, les sections obtenues sont les images de la base par l'homothétie de centre $S$ et de rapport $\dfrac{m}{h}$. Les aires de ces sections valent $\left(\dfrac{m}{h}\right)^2B$.

Donc tout plan parallèle aux bases coupera les pyramides en sections de même aire.

On déduit du Principe de Cavalieri que ces pyramides ont même volume.

Tout prisme droit à base triangulaire $ABCA'B'C'$ peut se décomposer en trois pyramides à base triangulaire : $ABCB'$, $A'B'C'C$ et $ACB'A'$.

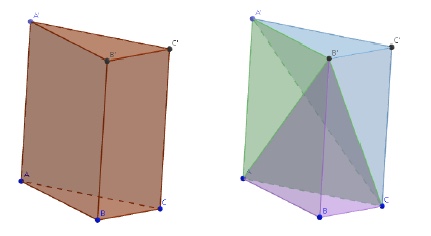
Les pyramides $ABCB'$ et $A'B'C'C$ ont même base  et même hauteur, on déduit du principe de Cavalieri qu'elles ont même volume.

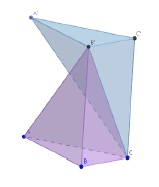
Les pyramides $A'B'C'C$ et $ACB'A'$ ont même base et même hauteur, on déduit du principe de Cavalieri qu'elles ont même volume.

Donc les pyramides $ABCB'$ et $A'B'C'C$ ont même volume et les pyramides $A'B'C'C$ et $ACB'A'$ ont même volume.
On en déduit que ces 3 pyramides ont même volume.  Ce volume est le tiers du volume du prisme.

Finalement la pyramide à base triangulaire dont la base vaut $B$ et la hauteur $h$ a pour volume le nombre $V=\frac{Bh}{3}$.

Notons tout d'abord que deux pyramides à bases triangulaires de même hauteur et dont l'aire de la base est la même ont même volume.

Remarquons ensuite que tout prisme droit à base triangulaire peut se décomposer en trois pyramides à base triangulaire.  Ces pyramides ont même aire de base et même hauteur deux à deux. On peut montrer en utilisant le principe de Cavalieri qu'elles ont même volume. Ce volume est le tiers du volume du prisme.

La pyramide à base triangulaire dont la base vaut $B$ et la hauteur $h$ a donc pour volume le nombre $V=\frac{Bh}{3}$.

Si la base de la pyramide est un polygone de surface $B$ à $n$ côtés, on la découpe en triangles. Chaque triangle constitue la base d'une pyramide ayant même sommet et même hauteur que la pyramide de départ. Chaque pyramide à base triangulaire a donc un volume égal à $V_i=\frac{B_ih}{3}$ où $B_i$ est l'aire du triangle de la base.  Le volume total de la pyramide de départ est donc $V=\displaystyle\sum_{i=1}^n\dfrac{B_ih}{3}=\dfrac{Bh}{3}.$

On va comparer le cône "tranche par tranche" avec une pyramide dont l'aire de la base et la hauteur sont les mêmes, ce qui revient à les couper par une infinité de plans parallèles à leur base. En coupant à toute hauteur on obtient des sections de même aire et on conclut du Principe de Cavalieri que ces deux solides ont même volume.

Le cône dont la base vaut $B$ et la hauteur $h$ a pour volume le nombre $V=\frac{Bh}{3}$.

On commence par emboîter les trois solides suivants : une demi-sphère de centre $O$ et de rayon $r$, un cylindre circonscrit à cette demi-sphère et un cône droit de dommet $O$ inscrit au cylindre.

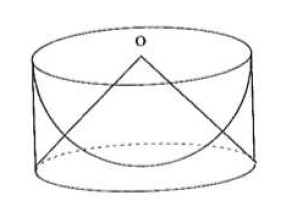
Le volume du cylindre de rayon $r$ et hauteur $r$ est $V_1=\pi r^3$ et le volume du cône de rayon $r$ et hauteur $r$ vaut $V_2=\frac{\pi r^3}{3}$. Appelons $V_3$ le volume de la demi-sphère.

On compare ensuite ces trois solides "tranche par tranche" en les coupant par des plans parallèles aux bases. Soit $\Pi$ un plan parallèle aux bases, qui coupe les trois solides à une distance $d$ du sommet du cône. Les trois sections obtenues sont des disques : disque de rayon $r_1$ et d'aire $A_1$ dans le cylindre, de rayon $r_2$ et d'aire $A_2$ dans le cône et de rayon $r_3$ et d'aire $A_3$ dans la demi-sphère.

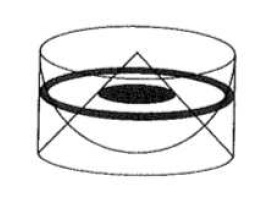
Pour déterminer ces rayons, coupons les trois solides par un plan qui contient l'axe du cylindre.

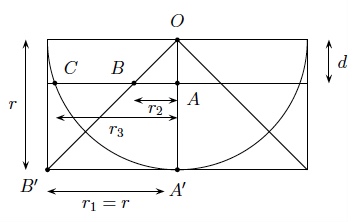
Le triangle $OAB$ est isocèle car il est semblable au triangle $OA'B'$ qui a deux côtés de longueur $r$. On déduit du Théorème de Thalès que $$\frac{r_2}{r}=\frac{d}{r}\hspace{1cm}\mbox{ et donc }\hspace{1cm}r_2=d.$$

Comme $r_1=r$ et que le triangle $OAC$ est rectangle, on déduit du Théorème de Pythagore que $$r_2^2+r_3^2=r^2.$$

En multipliant les deux membres de cette égalité par $\pi$, on obtient $$\pi r_2^2+\pi r_3^2=\pi r^2$$ ou encore $$A_1=A_2+A_3.$$  Cette égalité reste vraie quelle que soit la hauteur à laquelle on a coupé les solides. On déduit du Principe de Cavalieri que $V_1=V_2+V_3$. Donc $V_3=V_1-V_2=\pi r^3-\frac{\pi r^3}{3}=\frac{2}{3}\pi r^3$ et le volume de la sphère de rayon $r$ est $V=2V_3=\frac{4}{3}\pi r^3$.