Exercices résolus
Voici quelques exemples d'exercices résolus en détails.
-
Calculez le travail effectué en poussant une automobile sur une route d'un point $A$ à un point $B$ distants de 12m si la force d'intensité constante exercée est de 450 N.
$$W=\| \overrightarrow{\mbox{F}}\|\cdot d = 450\cdot 12= 5400 \mbox{ J}.$$
-
L'intensité et la direction d'une force constante sont données par $\overrightarrow{F}= (2,5)$. Calculez le travail effectué si le point d'application de la force se déplace de l'origine au point $P=(4,1)$.
On a $\overrightarrow{d}= (4,1)$ et donc $W=\overrightarrow{F}\odot\overrightarrow{d}= 2\cdot 4+5\cdot 1=13 \mbox{ Joules}.$
-
Sur un plan incliné dont la pente fait un angle de 30$^{\circ}$ avec l'horizontale, on pousse vers le haut un petit wagonnet pesant 500 N. Calculez le travail effectué pour compenser la force de gravitation si l'on pousse le wagonnet sur une distance de 24 m.
Représentons schématiquement le problème dans un système de coordonnées. Le vecteur $\overrightarrow{PQ}=(0,-500)$ représente la force de gravitation orientée vers le bas d'une intensité de 500 N. Le point d'application de cette force se déplace le long du vecteur $\overrightarrow{PR}$ de norme 24. Les composantes de ce vecteur sont : $a_1 = 24 \cos 30^{\circ}= 12\sqrt{3}$ et $a_2 = 24 \sin 30^{\circ}= 12$.
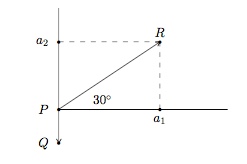
D'où, $W= (0,-500)\odot(12\sqrt{3}, 12)=-6000$.
Le travail effectué pour compenser la force de gravitation est donc de 6000 Joules.