Questions d'examen
Voici quelques questions qui ont été posées lors d'anciens examens et qui concernent ce chapitre.
Soit $A$, $B$ et $C$ trois points du plan $\mathbb{R}^2$.
-
Simplifiez au maximum l'écriture des vecteurs
$$\vec{u}=\overrightarrow{AC}+\overrightarrow{BA}+2\overrightarrow{CB}\mbox{ et }\vec{v}=2\overrightarrow{AC}-\overrightarrow{CB}+\overrightarrow{BA}-\overrightarrow{AB}.$$
On a \begin{array}{rcl} \vec{u}&=&\overrightarrow{AC}+\overrightarrow{BA}+2\overrightarrow{CB}\\ &=&\overrightarrow{BC}+2\overrightarrow{CB}\\ &=&-\overrightarrow{CB}+2\overrightarrow{CB}\\ &=&\overrightarrow{CB} \end{array}
et \begin{array}{rcl} \vec{v}&=&2\overrightarrow{AC}-\overrightarrow{CB}+\overrightarrow{BA}-\overrightarrow{AB}\\ &=&2\overrightarrow{AC}-\overrightarrow{CB}+2\overrightarrow{BA}\\ &=&2\overrightarrow{BC}+\overrightarrow{BC}\\ &=&3\overrightarrow{BC} \end{array}
-
Les vecteurs $\vec{u}$ et $\vec{v}$ sont-ils colinéaires ? Justifiez.
Les vecteurs $\vec{u}$ et $\vec{v}$ sont colin\'eaires car $\vec{v}=-3\vec{u}$.
Donnez les composantes horizontale et verticale d'un vecteur de longueur $4$ qui fait un angle de $75^{\circ}$ avec l'axe $OX$. Les valeurs de tous les nombres trigonométriques doivent être calculées.
$\overrightarrow{v}=(4\cos{75^{\circ}},4\sin{75^{\circ}})$.
Or \begin{array}{rcl} \cos{75^{\circ}}&=&\cos{(45^{\circ}+30^{\circ})}=\cos{45^{\circ}}\cos{30^{\circ}}-\sin{45^{\circ}}\sin{30^{\circ}}\\ &=&\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}\cdot \frac{1}{2}=\frac{1}{4}(\sqrt{6}-\sqrt{2}) \end{array}
et \begin{array}{rcl} \sin{75^{\circ}}&=&\sin{(45^{\circ}+30^{\circ})}=\sin{45^{\circ}}\cos{30^{\circ}}+\cos{45^{\circ}}\sin{30^{\circ}}\\ &=&\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot \frac{1}{2}=\frac{1}{4}(\sqrt{6}+\sqrt{2}) \end{array}
Donc $\overrightarrow{v}=(\sqrt{6}-\sqrt{2},\sqrt{6}+\sqrt{2})$.
On considère les points $P=(-1,3,-5)$, $Q=(2,k,-1)$ et $R=(m,0,-8)$ où $k$, $m\in\mathbb{R}$. Déterminez les valeurs des paramètres $k$ et $m$ telles que le triangle $PQR$ soit rectangle en $P$ et les côtés $PQ$ et $PR$ soient de même longueur.
On a \begin{array}{rcl} \mbox{le triangle }PQR\mbox{ est rectangle en }P&\Leftrightarrow&\overrightarrow{PQ}\perp\overrightarrow{PR}\\ &\Leftrightarrow&\overrightarrow{PQ}\odot\overrightarrow{PR}=0\\ &\Leftrightarrow&(3,k-3,4)\odot (m+1,-3,-3)=0\\ &\Leftrightarrow&3(m+1)-3(k-3)-12=0\\ &\Leftrightarrow&m=k \end{array}
De plus, \begin{array}{rcl} \Vert\overrightarrow{PQ}\Vert=\Vert\overrightarrow{PR}\Vert&\Leftrightarrow&\sqrt{9+(k-3)^2+16}=\sqrt{(m+1)^2+9+9}\\ &\Leftrightarrow&k^2-6k+16=m^2+2m+1 \end{array}
Puisque $m=k$, on en déduit $-6k+16=2k+1$ ou encore $k=m=\dfrac{15}{8}$.
Sachant que $\overrightarrow{AB}$ est de longueur $5$, $\overrightarrow{BD}$ est perpendiculaire à $\overrightarrow{AB}$ et de longueur double et $C$ est le milieu du segment qui relie $B$ à $D$, calculez $\overrightarrow{AC}\odot\overrightarrow{AD}$.
On peut représenter la situation par le schéma suivant
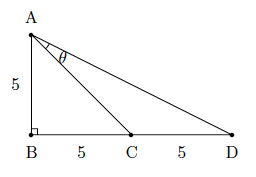
On déduit du théorème de Pythagore que
$$\Vert\overrightarrow{AC}\Vert^2=\Vert\overrightarrow{AB}\Vert^2+\Vert\overrightarrow{BC}\Vert^2=25+25=50$$
et donc $\Vert\overrightarrow{AC}\Vert=\sqrt{50}$.
De même
$$\Vert\overrightarrow{AD}\Vert^2=\Vert\overrightarrow{AB}\Vert^2+\Vert\overrightarrow{BD}\Vert^2=25+100=125$$
et donc $\Vert\overrightarrow{AD}\Vert=\sqrt{125}$.
Par la règle des cosinus, on a
$$\Vert\overrightarrow{CD}\Vert^2=\Vert\overrightarrow{AC}\Vert^2+\Vert\overrightarrow{AD}\Vert^2-2\Vert\overrightarrow{AC}\Vert\cdot\Vert\overrightarrow{AD}\Vert\cdot\cos{\theta}$$
d'où $\cos{\theta}=\dfrac{150}{2\sqrt{125}\sqrt{50}}$.
Comme
$$\overrightarrow{AC}\odot\overrightarrow{AD}=\Vert\overrightarrow{AC}\Vert\cdot\Vert\overrightarrow{AD}\Vert\cdot\cos{\theta}$$
on obtient finalement
$$\overrightarrow{AC}\odot\overrightarrow{AD}=\sqrt{50}\sqrt{125}\dfrac{150}{2\sqrt{125}\sqrt{50}}=75.$$
On considère le parallélipipède rectangle ci-dessous. Déterminez les coordonnées des sommets $C$, $G$ et $H$ ainsi que le volume de ce parallélipipède.
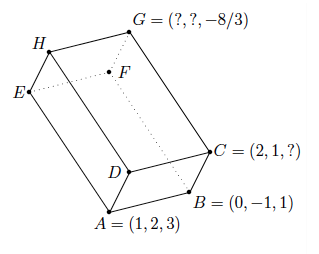
$\bullet$ Soit $C=(2,1,z)$. On a $\overrightarrow{AB}\perp\overrightarrow{BC}$ et donc
$$\overrightarrow{AB}\odot\overrightarrow{BC}=(-1,-3,-2)\odot(2,2,z-1)=0.$$
On en déduit $-2-6-2z+2=0$ d'où $z=-3$ et $C=(2,1,-3)$.
$\bullet$ Soit $G=(x,y,-\frac{8}{3})$. On a $\overrightarrow{CG}\perp$ plan $ABC$ donc $\overrightarrow{CG}=k\vec{n}$ où $\vec{n}$ est le vecteur normal au plan. Vu que
$$\vec{n}=\overrightarrow{AB}\times\overrightarrow{BC}=(-1,-3,-2)\times (2,2,-4)=(16,-8,4),$$
on a $\overrightarrow{CG}=(x-2,y-1,-\frac{8}{3}+3)=k(16,-8,4)$. On en déduit $k=\frac{1}{12}$ et donc $G=\left(\dfrac{10}{3},\dfrac{1}{3},-\dfrac{8}{3}\right)$.
$\bullet$ Soit $H=(x,y,z)$. On a $\overrightarrow{GH}=\overrightarrow{BA}$ d'où
$$\overrightarrow{GH}=\left(x-\frac{10}{3},y-\frac{1}{3},z+\frac{8}{3}\right)=(1,3,2).$$
On en déduit $H=\left(\dfrac{13}{3},\dfrac{10}{3},-\dfrac{2}{3}\right)$.
$\bullet$ Le volume du parallélipipède construit sur les vecteurs $\overrightarrow{AB}$, $\overrightarrow{BC}$ et $\overrightarrow{CG}$ est donné par $V=\Vert\overrightarrow{AB}\Vert\cdot \Vert\overrightarrow{BC}\Vert\cdot \Vert\overrightarrow{CG}\Vert$ et donc \begin{array}{rcl} V&=&\sqrt{1+9+4}\cdot \sqrt{4+4+16}\cdot \sqrt{\frac{16}{9}+\frac{4}{9}+\frac{1}{9}}\\ &=&\sqrt{14\cdot 24\cdot\frac{21}{9}}=\sqrt{784}=28. \end{array}