Questions de théorie

Un repère dans le plan est la donnée d'une origine $O$ et de deux vecteurs $\vec{e_1}$ et $\vec{e_2}$ non parallèles. Un tel repère sera noté $[O; \vec{e_1}, \vec{e_2}]$.

Le repère $[O; \vec{e_1}, \vec{e_2}]$ est orthonormé si les vecteurs $\vec{e_1}$ et $\vec{e_2}$ sont perpendiculaires et de longueur $1$.

Le repère $[(0,0);(1,0),(0,1)]$ est appelé repère canonique de $\mathbb{R}^2$. C'est un repère cartésien orthonormé.

Les vecteurs $(1,0)$ et $(0,1)$ sont appelés vecteurs de base car on peut écrire n'importe quel autre vecteur comme combinaison linéaire de ces deux vecteurs : $$\vec{v}=(v_x,v_y)=v_x(1,0)+v_y(0,1).$$

La composante horizontale du vecteur $(a,b)$ est le nombre réel $a$ et la composante verticale du vecteur $(a,b)$ est le nombre réel $b$.

Un repère dans l'espace est la donnée d'une origine $O$ et de trois vecteurs $\vec{e_1}$, $\vec{e_2}$ et $\vec{e_3}$ non coplanaires. Un tel repère sera noté $[O; \vec{e_1}, \vec{e_2}, \vec{e_3}]$.

Le repère $[O; \vec{e_1}, \vec{e_2}, \vec{e_3}]$ est orthonormé si les vecteurs $\vec{e_1}$, $\vec{e_2}$ et $\vec{e_3}$ sont orthogonaux deux à deux et de longueur $1$.

Le repère $[(0,0,0);(1,0,0),(0,1,0),(0,0,1)]$ est appelé repère canonique de $\mathbb{R}^3$. C'est un repère cartésien orthonormé.

Les vecteurs $(1,0,0)$, $(0,1,0)$ et $(0,0,1)$ sont appelés vecteurs de base car on peut écrire n'importe quel autre vecteur comme combinaison linéaire de ces trois vecteurs : $$\vec{v}=(v_x,v_y,v_z)=v_x(1,0,0)+v_y(0,1,0)+v_z(0,0,1).$$

Une surface donnée peut se trouver décrite par une équation compliquée si on travaille par rapport à un repère donné alors que par rapport à un repère mieux choisi elle serait décrite par une équation nettement plus simple.

Faire un changement de repère permet donc de simplifier les équations avec lesquelles on travaille.

Le changement de repère par translation consiste à translater l'origine du repère sans changer l'orientation des axes.  Ce type de changement de repère permet de supprimer les termes du premier degré d'une équation.

Le changement de repère par rotation consiste à faire tourner le repère autour d'un de ses axes.  Ce type de changement de repère permet de supprimer les termes "mixtes" ($xy$, $xz$ et $yz$) d'une équation.

Dans le changement de repère par translation, on change l'origine, mais on garde la même base pour l'espace des flèches.

Soit $[0; \vec e_1,\vec e_2,\vec e_3]$ le 1er repère et $O'$ la nouvelle origine, avec comme coordonnées $(x_0,y_0,z_0)$ dans le repère initial.

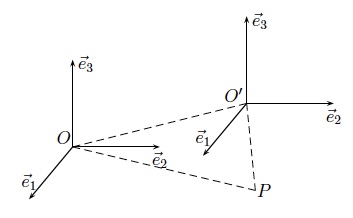
Soit alors $P$ un point quelconque de coordonnées $(x,y,z)$ dans le 1er repère et $(x',y',z')$ dans le second. On a $$\overrightarrow{OP} = \overrightarrow{OO'}+ \overrightarrow{O'P}.$$ En termes de coordonnées, cela donne $$ \left\{ \begin{array}{l} x = x_0 + x' \\ y = y_0 + y' \\ z = z_0 + z' \end{array} \right. $$

Ces formules permettent de passer facilement d'un repère à l'autre.

Dans le changement de repère par rotation, on garde la même origine mais on fait tourner le repère autour d'un axe de coordonnées.

Soit $OABC$ un repère cartésien orthonormé.  Faisons par exemple une rotation d'amplitude $\alpha$ dans le sens antihorlogique autour de $OA$.

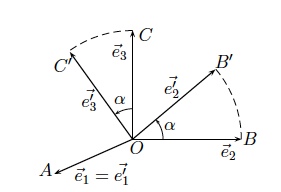
On a facilement l'expression de la nouvelle base en fonction de l'ancienne : $$ \begin{array}{rcl} \vec e'_1& =& \vec e_1\\ \vec e'_2 &=& 0 \, \vec e_1 + (\cos \alpha) \, \vec e_2 + (\sin \alpha)\, \vec e_3 \\ \vec e'_3 &=& 0 \, \vec e_1 + (- \sin \alpha)\, \vec e_2 + (\cos \alpha)\, \vec e_3 \end{array} $$

d'où $$ \left\{ \begin{array}{l} x = x' \\ y =(\cos \alpha)\, y' - (\sin \alpha)\, z' \\ z = (\sin \alpha)\, y' + (\cos \alpha)\, z' \end{array} \right. $$

On a $$ \begin{array}{rcl} \vec{e'_1}& =& \vec e_1\\[2mm] \vec{e'_2} &=& 0 \, \vec e_1 + (\cos \alpha)\, \vec e_2 + (\sin \alpha)\, \vec e_3 \\[2mm] \vec{e'_3} &=& 0 \, \vec e_1 + (- \sin \alpha)\, \vec e_2 + (\cos \alpha)\, \vec e_3 \end{array} $$

Donc $$ \left\{ \begin{array}{rcl} \vec{e'_1}& =& \vec e_1\\[2mm] \vec{e'_2} &=& \cos \alpha\, \vec e_2 + \sin \alpha\, \vec e_3 \\[2mm] \vec{e'_3} &=&- \sin \alpha\, \vec e_2 + \cos \alpha\, \vec e_3 \end{array} \right. $$

Dans le repère initial $\mathcal{R}$ : $P=(x,y,z)$ c'est-à-dire $\overrightarrow{OP}=x\vec e_1+y\vec e_2+z\vec e_3$.

Dans le nouveau repère $\mathcal{R'}$ : $P=(x',y',z')$ c'est-à-dire $\overrightarrow{OP}=x'\vec{e'_1}+y'\vec{e'_2}+z'\vec{e'_3} $.

Donc $$ \begin{array}{rcl} x\vec e_1+y\vec e_2+z\vec e_3&=&x'\vec{e'_1}+y'\vec{e'_2}+z'\vec{e'_3}\\[2mm] &=&x'\vec{e_1}+y'(\cos \alpha\, \vec e_2 + \sin \alpha\, \vec e_3)+z'(- \sin \alpha\, \vec e_2 + \cos \alpha\, \vec e_3)\\[2mm] &=&x'\vec{e_1}+(y'\cos \alpha-z'\sin \alpha)\, \vec e_2+(y'\sin \alpha+z'\cos \alpha)\, \vec e_3 \end{array} $$

Passage de $\mathcal{R'}$ vers $\mathcal{R}$ :
$$ \left\{ \begin{array}{l} x =x' \\ y = y'\cos \alpha-z'\sin \alpha\\ z = y'\sin \alpha+z'\cos \alpha\end{array} \right. $$

On a $$ \begin{array}{rcl} \vec{e'_1}& =&(\cos \alpha)\, \vec e_1+0 \, \vec e_2 + (- \sin \alpha)\, \vec e_3 \\[2mm] \vec{e'_2} &=&\vec e_2\\[2mm] \vec{e'_3} &=& (\sin \alpha)\, \vec e_1 + 0 \, \vec e_2 +(\cos \alpha)\, \vec e_3 \end{array} $$

Donc $$ \left\{ \begin{array}{rcl} \vec{e'_1}& =&\cos \alpha\, \vec e_1- \sin \alpha\, \vec e_3 \\[2mm] \vec{e'_2} &=&\vec e_2\\[2mm] \vec{e'_3} &=& \sin \alpha\, \vec e_1 + \cos \alpha\, \vec e_3\end{array} \right. $$

Dans le repère initial $\mathcal{R}$ : $P=(x,y,z)$ c'est-à-dire $\overrightarrow{OP}=x\vec e_1+y\vec e_2+z\vec e_3$.

Dans le nouveau repère $\mathcal{R'}$ : $P=(x',y',z')$ c'est-à-dire $\overrightarrow{OP}=x'\vec{e'_1}+y'\vec{e'_2}+z'\vec{e'_3} $.

Donc $$ \begin{array}{rcl} x\vec e_1+y\vec e_2+z\vec e_3&=&x'\vec{e'_1}+y'\vec{e'_2}+z'\vec{e'_3}\\[2mm] &=&x'(\cos \alpha\, \vec e_1- \sin \alpha\, \vec e_3)+y'\vec e_2+z'(\sin \alpha\, \vec e_1 + \cos \alpha\, \vec e_3)\\[2mm] &=&(x'\cos \alpha+z'\sin \alpha)\, \vec e_1+y'\, \vec e_2+(-x'\sin \alpha+z'\cos \alpha)\, \vec e_3 \end{array} $$

Passage de $\mathcal{R'}$ vers $\mathcal{R}$ :
$$ \left\{ \begin{array}{l} x =x'\cos \alpha+z'\sin \alpha \\ y = y'\\ z = -x'\sin \alpha+z'\cos \alpha\end{array} \right. $$

On a $$ \begin{array}{rcl} \vec{e'_1}& =&(\cos \alpha)\, \vec e_1 + (\sin \alpha)\, \vec e_2+0 \, \vec e_3\\[2mm] \vec{e'_2} &=& (- \sin \alpha)\, \vec e_1+ (\cos \alpha)\, \vec e_2 +0 \, \vec e_3 \\[2mm] \vec{e'_3} &=&\vec e_3 \end{array} $$

Donc $$ \left\{ \begin{array}{rcl} \vec{e'_1}& =&\cos \alpha\, \vec e_1 + \sin \alpha\, \vec e_2\\[2mm] \vec{e'_2} &=& - \sin \alpha\, \vec e_1+ \cos \alpha\, \vec e_2 \\[2mm] \vec{e'_3} &=&\vec e_3 \end{array} \right. $$

Dans le repère initial $\mathcal{R}$ : $P=(x,y,z)$ c'est-à-dire $\overrightarrow{OP}=x\vec e_1+y\vec e_2+z\vec e_3$.

Dans le nouveau repère $\mathcal{R'}$ : $P=(x',y',z')$ c'est-à-dire $\overrightarrow{OP}=x'\vec{e'_1}+y'\vec{e'_2}+z'\vec{e'_3} $.

Donc $$ \begin{array}{rcl} x\vec e_1+y\vec e_2+z\vec e_3&=&x'\vec{e'_1}+y'\vec{e'_2}+z'\vec{e'_3}\\[2mm] &=&x'(\cos \alpha\, \vec e_1 + \sin \alpha\, \vec e_2)+y'(- \sin \alpha\, \vec e_1+ \cos \alpha\, \vec e_2)+z'\, \vec e_3\\[2mm] &=&(x'\cos \alpha-y' \sin \alpha)\, \vec{e_1}+(x'\sin \alpha+y'\cos \alpha)\, \vec e_2+z'\, \vec e_3 \end{array} $$

Passage de $\mathcal{R'}$ vers $\mathcal{R}$ :
$$ \left\{ \begin{array}{l} x =x'\cos \alpha-y' \sin \alpha \\ y = x'\sin \alpha+y'\cos \alpha\\ z =z'\end{array} \right. $$