Définitions
- Amplitude d'un angle
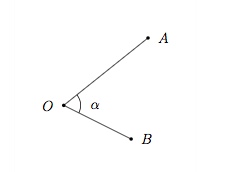
La mesure d'un angle $\alpha$, ou amplitude de l'angle, est la mesure de longueur $s$ de l'arc $AB$, où $A$ et $B$ se trouvent sur le cercle unité centré en $O$.
- Angle
Un angle est une portion du plan comprise entre deux demi-droites. Il est composé de deux côtés ayant un même sommet. Si $O$ est le sommet et $A$, $B$ sont deux points sur les côtés, on parlera de l'angle $\widehat{AOB}$.
- Angle aigu
Un angle est aigu si son amplitude est inférieure à $90^{\circ}$.
- Angle au centre
Un angle au centre d'un cercle a le centre de ce cercle comme sommet.
- Angle droit
Un angle droit est un angle dont l'amplitude est $90^{\circ}$.
- Angle entre deux vecteurs
Si $\theta$ désigne l'angle entre les deux vecteurs non nuls $\vec{u}$ et $\vec{v}$, alors
$$\begin{array}[t]{c} \cos\theta = \displaystyle\frac{\vec{u}\odot\vec{v}}{\|\vec{u}\|\|\vec{v}\|} \end{array}$$
- Angle inscrit
Un angle est inscrit dans un cercle si son sommet est un point du cercle et si ses deux côtés coupent le cercle en un deuxième point.
- Angle obtu
Un angle est obtu si son amplitude est entre $90^{\circ}$ et $180^{\circ}$.
- Angle plat
Un angle plat est un angle dont l'amplitude est $180^{\circ}$.
- Angles adjacents
Deux angles sont adjacents s'ils ont le même sommet et un côté commun.
- Angles alternes externes
Considérons deux droites parallèles $d_1$ et $d_2$ coupées par une droite $d_3$.
Deux angles sont alternes externes s'ils n'ont pas le même sommet et se trouvent de part et d'autre de la droite $d_3$ et à l'extérieur des droites $d_1$ et $d_2$.
- Angles alternes internes
Considérons deux droites parallèles $d_1$ et $d_2$ coupées par une droite $d_3$.
Deux angles sont alternes internes s'ils n'ont pas le même sommet et se trouvent de part et d'autre de la droite $d_3$ et entre les droites $d_1$ et $d_2$.
- Angles anti-supplémentaires
Deux angles dont la différence des amplitudes vaut $180^\circ$ sont dits anti-supplémentaires.
- Angles complémentaires
Des angles sont complémentaires si la somme de leurs amplitudes vaut $90^{\circ}$.
- Angles congruents
Deux angles ayant même amplitude sont dits congruents.
- Angles correspondants
Considérons deux droites parallèles $d_1$ et $d_2$ coupées par une droite $d_3$.
Deux angles sont correspondants s'ils n'ont pas le même sommet et se trouvent du même côté de la droite $d_3$ et du même côté respectivement de la droite $d_1$ et de la droite $d_2$.
- Angles équivalents
Deux angles sont équivalents si la différence d'amplitude de ces angles est un multiple de $360^\circ = 2\pi$ radians.
- Angles opposés
Deux angles sont opposés si la somme de leurs amplitudes vaut $0^{\circ}$.
- Angles opposés par le sommet
Deux angles sont opposés par le sommet s'ils ont même sommet et si leurs côtés sont les prolongements respectifs l'un de l'autre.
- Angles supplémentaires
Des angles sont suplémentaires si la somme de leurs amplitudes vaut $180^{\circ}$.
- Arc de cercle
Soit $P$ et $Q$ deux points d'un cercle. L' arc de cercle $PQ$ est la partie du cercle délimitée par les points $P$ et $Q$.
- Bissectrice d'un angle
La bissectrice d'un angle est la droite qui coupe cet angle en deux angles de même amplitude.
- Bissectrice d'un triangle
Une bissectrice d'un triangle est une droite qui coupe un de ses angles en deux angles de même amplitude.
- Carré
Un carré est un quadrilatère qui a quatre côtés de même longueur et quatre angles droits.
- Centre de gravité
Le centre de gravité d'un triangle est le point d'intesection de ses médianes.
- Cercle
Dans un plan fixé, on se donne un point $C$ et un nombre $r>0$. On appelle cercle de centre $C$ et de rayon $r$, l'ensemble des points du plan qui sont à une distance $r$ du point $C$. C'est donc l'ensemble des points $P$ du plan qui vérifient la condition $$d(P,C)=r.$$
- Cercle circonscrit
Le cercle circonscrit à un triangle est le cercle qui passe par ses 3 sommets.
- Cercle inscrit
Le cercle inscrit à un triangle est le cercle qui est tangent aux 3 côtés du triangle.
- Cercles concentriques
On dira que des cercles sont concentriques s'ils ont le même centre.
- Composantes d'un vecteur
Si $(x_a,y_a,z_a)$ et $(x_b,y_b,z_b)$ sont respectivement les coordonnées des points $A$ et $B$, le vecteur $\overrightarrow{AB}$ a pour composantes $(x_b-x_a,y_b-y_a,z_b-z_a)$.
- Cône
Un cône est un solide obtenu en joignant les points d'une courbe fermée plane à un point fixé extérieur au plan de la courbe. Le point fixé est appelé sommet du cône et la surface entourée par la courbe fermée est la base du cône. La hauteur du cône est la longueur du segment de droite mené du sommet perpendiculairement à la base et limité par le sommet et la base.
- Cône circulaire droit
Un cône circulaire droit est un solide engendré par la rotation d'un triangle rectangle autour d'un côté de l'angle droit.
- Coordonnées cartésiennes
D'un point $P$ quelconque du plan, on mène des parallèles aux axes qui coupent ceux-ci en $a$ pour l'axe des $x$ et en $b$ pour l'axe des $y$. Le point $P$ est ainsi associé au couple de nombres réels $(a,b)$.
Inversément, à tout couple de nombres réels $(a,b)$, en menant des parallèles aux axes passant par $a$ porté sur l'axe des $x$ et par $b$ porté sur l'axe des $y$, on fait correspondre l'unique point d'intersection de ces deux droites.
Le couple $(a,b)$ est appelé coordonnées cartésiennes du point $P$. Le nombre $a$ est l'abscisse de $P$ et le nombre $b$ est son ordonnée.
- Coordonnées cylindriques
Dans l'espace $\mathbb{R}^3$, les coordonnées cylindriques d'un point $P$ sont la donnée de
$\bullet\, $ la cote $z$,
$\bullet\, $ la distance de $P$ à l'origine, notée $r$ ($r>0$),
$\bullet\, $ l'angle entre l'axe $OX$ et $OP$, noté $\theta $ ($\theta\in [0,2\pi[\, )$.
- Coordonnées polaires
Dans le plan $\mathbb{R}^2$, les coordonnées polaires d'un point $P$ sont la donnée de
$\bullet\, $ la distance de $P$ à l'origine, notée $r$ ($r>0$),
$\bullet\, $ l'angle entre l'axe $OX$ et $OP$, noté $\theta $ (par convention, $\theta\in [0,2\pi[\, $).
- Coordonnées sphériques
Dans l'espace $\mathbb{R}^3$, les coordonnées sphériques d'un point $P$ sont la donnée de
$\bullet\, $ la distance du point $P$ à l'origine, notée $r$ ($r>0$),
$\bullet\, $ l'angle que fait le demi-plan comprenant $OZ$ et $P$ avec le demi-plan $OXZ$, appelé longitude et noté $\varphi$,
$\bullet\, $ l'angle que fait $OP$ avec $OZ$, appelé co-latitude et noté $\theta$ (la latitude se compte à partir de l'équateur).
- Corde
Soit $P$ et $Q$ deux points d'un cercle. La corde $[PQ]$ est le segment joignant $P$ à $Q$.
- Cube
Un cube est un polyèdre dont la surface est constituée de 6 faces carrées isométriques. Il fait partie des polyèdres réguliers et est constitué de 6 faces, 8 sommets et 12 arêtes.
- Cylindre
Un cylindre est un solide engendré par la translation qui amène une surface fermée sur une autre surface superposable à la première et situées dans des plans parallèles distincts. Les deux surfaces sont appelées bases du cylindre.
- Cylindre circulaire
Un cylindre circulaire est un solide engendré par la translation qui amène un disque sur un autre disque de même rayon situés dans des plans parallèles distincts.
- Cylindre circulaire droit
Un cylindre circulaire droit est un solide engendré par la rotation d'un rectangle autour d'un de ses côtés. Le cylindre est délimité par deux disques appelés bases et par une surface non plane appelée surface latérale.
- Cylindre droit
Un cylindre droit est un solide borné par une région plane $B_1$, appelée la base et une région identique $B_2$ dans un plan parallèle. Le cylindre est constitué de tous les points des segments perpendiculaires à la base qui
relient $B_1$ à $B_2$.
- Développement
Le développement ou patron d'un solide est la figure plane obtenue par la mise à plat de sa surface. Le développement est une figure plane telle que si on la plie aux endroits appropriés, on obtient un solide en collant entre eux les bords libres.
- Diagonale d'un quadrilatère
Une diagonale d'un quadrilatère est un segment de droite qui relie deux sommets opposés.
- Diamètre
Le diamètre d'un cercle est un segment qui passe par son centre et a pour extrémités deux points du cercle.
- Différence de deux vecteurs
Si $\vec{u}$ est le vecteur $(u_x,u_y,u_z)$ et $\vec{v}$ le vecteur $(v_x,v_y,v_z)$ alors le vecteur $\overrightarrow{u-v}$ est donné par $$\overrightarrow{u-v}=(u_x-v_x,u_y-v_y,u_z-v_z).$$
- Direction d'un plan
Soit $P_1 = (x_1,y_1,z_1 )$, $P_2 = (x_2,y_2,z_2 )$ et $P_3 = (x_3,y_3,z_3 )$ trois points distincts de $\mathbb{R}^3$. La direction du plan $\Pi$ contenant ces trois points est déterminée par les vecteurs $\overrightarrow{P_1P_2}=(x_2-x_1,y_2-y_1,z_2-z_1)$ et $\overrightarrow{P_1P_3}=(x_3-x_1,y_3-y_1,z_3-z_1)$.
- Direction d'une droite
Soit $P_1 = (x_1,y_1,z_1 )$ et $P_2 = (x_2,y_2,z_2 )$ deux points distincts de $\mathbb{R}^3$. La direction de la droite $\Delta$ contenant ces deux points est déterminée par le vecteur $\overrightarrow{P_1P_2}=(x_2-x_1,y_2-y_1,z_2-z_1)$. Le vecteur $\overrightarrow{P_1P_2}$ est appelé vecteur directeur de la droite.
- Disque
Le disque de centre $C$ et de rayon $r$ est l'ensemble des points du plan situés à distance inférieure ou égale à $r$ du point $C$.
- Distance
Dans $\mathbb{R}^2$, la distance entre deux points $P=(x_p,y_p)$ et $Q=(x_q,y_q)$ est donnée par la formule $$ \mbox{d(P,Q)}= \sqrt{(x_q -x_p)^2 +(y_q-y_p)^2}. $$
Dans $\mathbb{R}^3$, la distance entre deux points $P=(x_p,y_p,z_p)$ et $Q=(x_q,y_q,z_q)$ est donnée par la formule $$ \mbox{d(P,Q)}= \sqrt{(x_q -x_p)^2 +(y_q-y_p)^2+(z_q-z_p)^2}. $$
- Dodécaèdre
Le dodécaèdre est un polyèdre régulier constitué de 12 faces, 20 sommets et 30 arêtes. Ses faces sont des pentagones réguliers.
- Droite d'Euler
La droite d'Euler est la droite qui contient le centre de gravité, l'orthocentre et le centre du cercle circonscrit à un triangle.
- Droite de l'espace
Une droite de $\mathbb{R}^3$ est vue comme l'intersection de deux plans. Dans $\mathbb{R}^3$, une droite est donc caractérisée par deux équations de plans $$ \left\{\begin{array}{c}a_1x+b_1y+c_1z+d_1=0\\ a_2x+b_2y+c_2z+d_2=0 \end{array}\right. $$
- Equation trigonométrique
Une équation trigonométrique est une équation où l'inconnue intervient dans l'expression d'un sinus, d'un cosinus, d'une tangente ou d'une cotangente.
Equation fondamentale : équation du type
$\sin x = m$ avec $m \in [-1,1]$,
$\cos x = m$ avec $m \in [-1,1]$,
$\mbox{tg }x = m$ avec $m \in \mathbb{R}$.
Equation élémentaire : équation du type
$\sin x = \sin \alpha$,
$\cos x = \cos \alpha$,
$\mbox{tg }x = \mbox{tg }\alpha$.
- Hauteur d'un triangle
Une hauteur d'un triangle est une droite passant par un sommet et perpendiculaire au côté opposé (ou à son prolongement).
- Hypoténuse
L'hypoténuse est le côté opposé à l'angle droit dans un triangle rectangle.
- Icosaèdre
L'icosaèdre est un polyèdre régulier constitué de 20 faces, 12 sommets et 30 arêtes. Ses faces sont des triangles équilatéraux.
- Losange
Un losange est un quadrilatère qui possède quatre côtés de même longueur.
- Médiane d'un quadrilatère
Une médiane d'un quadrilatère est un segment de droite qui relie les milieux de deux côtés opposés.
- Médiane d'un triangle
Une médiane d'un triangle est une droite qui relie un des sommets au milieu du côté opposé.
- Médiatrice d'un segment
La médiatrice d'un segment est la droite perpendiculaire au milieu de ce segment.
- Médiatrice d'un triangle
Une médiatrice d'un triangle est une droite perpendiculaire au milieu d'un de ses côtés.
- Norme d'un vecteur
La norme du vecteur $\vec{v}=(v_x,v_y,v_z)$ est le nombre réel positif donné par $$\|\vec{v}\| =\sqrt{v_x^2+v_y^2+v_z^2}.$$
Si $\vec{u}=\overrightarrow{AB}=(x_b-x_a,y_b-y_a,z_b-z_a)$ alors $$\|\vec{u}\| =\|\overrightarrow{AB}\| =\sqrt{(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2}.$$
- Octaèdre
L'octaèdre est un polyèdre régulier constitué de 8 faces, 6 sommets et 12 arêtes. Ses faces sont des triangles équilatéraux.
- Orthocentre
L'orthocentre d'un triangle est l'intersection de ses hauteurs.
- Parallélipipède
Un parallélipipède est un prisme dont les bases sont des parallélogrammes isométriques.
- Parallélipipède rectangle
Un parallélipipède rectangle est un prisme droit à bases rectangulaires.
- Parallélogramme
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles. Les côtés opposés d'un parallélogramme ont même longueur et ses angles opposés ont même amplitude.
- Plan de l'espace
Un plan de $\mathbb{R}^3$ est déterminé par une équation du premier degré liant les variables $x$, $y$ et $z$ : $$ax+by+cz+d=0.$$
- Point milieu
Si $P = (x_p,y_p,z_p) $ et $Q = (x_q,y_q,z_q)$ alors les coordonnées du point $M$, milieu du vecteur $\overrightarrow{PQ}$ sont données par $$(x_m,y_m,z_m) =\left(\frac{1}{2} (x_p + x_q),\frac{1}{2} (y_p+ y_q),\frac{1}{2} (z_p+ z_q)\right).$$
- Polyèdre
Un polyèdre est un solide limité de toutes parts par des portions de plans. Les faces d'un polyèdre sont les polygones plans qui composent la surface du polyèdre. Les arêtes d'un polyèdre sont les côtés des polygones qui forment les faces du polyèdre. Les sommets du polyèdre sont les extrémités des arêtes.
- Polyèdre convexe
Un polyèdre est convexe si tout segment ayant ses extrémités dans le polyèdre y est inclus tout entier.
- Polyèdre régulier
Un polyèdre régulier est un polyèdre convexe constitué de polygones réguliers isométriques en même nombre autour de chaque sommet.
- Polygone
Un polygone est une figure plane délimitée par une ligne fermée constituée de segments de droite. Ces segments sont les côtés du polygone et le point d'intersection de deux côtés est appelé sommet du polygone. Une diagonale d'un polygone est un segment de droite qui joint deux sommets non consécutifs.
- Polygone convexe
Un polygone est convexe si tout segment ayant ses extrémités sur le polygône y est inclus tout entier.
- Polygone régulier
Un polygone est régulier si tous ses côtés ont même longueur et tous ses angles intérieurs ont même amplitude.
- Prisme
Un prisme est un polyèdre ayant pour base deux polygones égaux et parallèles et dont les faces latérales sont des parallélogrammes. Les deux polygones translatés sont les bases du prisme et les parallélogrammes sont appelés faces latérales. La hauteur d'un prisme est la distance entre les plans des bases. C'est la hauteur de la perpendiculaire commune aux deux bases.
- Prisme droit
Un prisme est droit lorsque les arêtes latérales sont perpendiculaires à la base.
- Produit mixte de trois vecteurs
Le produit mixte des 3 vecteurs $\vec u$, $\vec v $ et $\vec w $ est le nombre réel $$(\vec u \times \vec v) \odot \vec w .$$
- Produit scalaire de deux vecteurs
Si $\vec{u}=(u_x,u_y,u_z)$ et $\vec{v}=(v_x,v_y,v_z)$ alors le produit scalaire de $\vec u$ et $\vec v$ est le nombre réel $$\vec{u}\odot\vec{v}=u_x v_x + u_y v_y + u_z v_z.$$
- Produit vectoriel de deux vecteurs
Le produit vectoriel de deux vecteurs $\vec{u}$ et $\vec{v}$ est le vecteur $\vec{u}\times\vec{v}$ qui satisfait les propriétés suivantes :
$\bullet\,\, \vec{u}\times\vec{v}$ est perpendiculaire à $\vec{u}$ et à $\vec{v}$;
$\bullet\,\, \|\vec{u}\times\vec{v}\|=\|\vec{u}\|\|\vec{v}\|\,|\sin{\theta}| $;
$\bullet\,\, $ les vecteurs $\vec{u}$, $\vec{v}$ et $\vec{u}\times\vec{v}$ pris dans cet ordre forment un repère d'orientation directe.
Si $\vec{u}=(u_x,u_y,u_z)$ et $\vec{v}=(v_x,v_y,v_z)$, les composantes du vecteur $\vec{u}\times\vec{v}$ sont données par
$$\vec{u}\times\vec{v}=(u_yv_z-u_zv_y,u_zv_x-u_xv_z, u_xv_y-u_yv_x).$$
- Projection orthogonale
On note $\mbox{comp}_u\vec{v}$ la composante du vecteur $\vec{v}$ suivant le vecteur $\vec{u}$. C'est la longueur du vecteur qui est la projection orthogonale de $\vec{v}$ sur $\vec{u}$ si cette projection orthogonale a le même sens que $\vec{u}$, l'opposé de cette longueur dans le cas contraire.
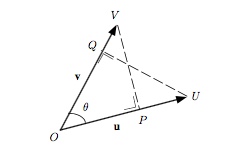
On a
$$\mbox{comp}_u\vec{v}=\displaystyle\frac{\vec{u}\odot\vec{v}}{\|\vec{u}\|}.$$
- Pyramide
Une pyramide est un polyèdre dont la surface est constituée d'un polygone à $n$ côtés appelé base et de $n$ triangles ayant chacun un côté commun avec la base et ayant tous un point commun n'appartenant pas au plan de la base. Le sommet de la pyramide est le point commun aux $n$ triangles. Sa hauteur est la longueur du segment de droite mené du sommet perpendiculairement à la base et limité par le sommet et la base.
- Quadrilatère
Un quadrilatère est un polygone à quatre côtés.
- Rectangle
Un rectangle est un quadrilatère qui a quatre angles droits.
- Repère cartésien orthonormé
Un repère dans le plan est la donnée d'une origine $O$ et de deux vecteurs $\vec{e_1}$ et $\vec{e_2}$ non parallèles. Un tel repère sera noté $[O; \vec{e_1}, \vec{e_2}]$.
Le repère $[O; \vec{e_1}, \vec{e_2}]$ est orthonormé si les vecteurs $\vec{e_1}$ et $\vec{e_2}$ sont perpendiculaires et de longueur $1$.
Un repère dans l'espace est la donnée d'une origine $O$ et de trois vecteurs $\vec{e_1}$, $\vec{e_2}$ et $\vec{e_3}$ non coplanaires. Un tel repère sera noté $[O; \vec{e_1}, \vec{e_2}, \vec{e_3}]$.
Le repère $[O; \vec{e_1}, \vec{e_2}, \vec{e_3}]$ est orthonormé si les vecteurs $\vec{e_1}$, $\vec{e_2}$ et $\vec{e_3}$ sont orthogonaux deux à deux et de longueur $1$.
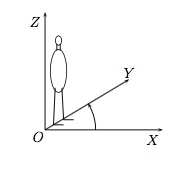
- Repère droit
On dit que le repère formé par les axes $OX$, $OY$ et $OZ$ est droit ou d'orientation directe si un spectateur ''debout'' sur le plan $OXY$, les pieds en $O$ et la tête en $Z$, observe que pour amener la droite $OX$ sur la droite $OY$, il doit faire une rotation dans le sens antihorlogique (on regarde le plus petit angle possible). Dans le cas contraire, on parle de repère gauche.
- Secteur circulaire
On appelle secteur circulaire la portion de disque comprise entre un arc et les 2 rayons qui aboutissent à ses extrémités.
- Segment circulaire
On appelle segment circulaire la portion de disque comprise entre un arc et la corde qui le sous-tend.
- Solide de révolution
Un solide de révolution est un solide obtenu en faisant tourner une surface plane autour d'une droite, appelée axe de rotation, cette droite étant située dans le plan de la surface.
- Solides d'Archimède
Les solides d'Archimède sont des polyèdres convexes dont les faces sont composées d'au moins deux sortes de polygones réguliers convexes, dont les arêtes ont toutes la même longueur et tels qu'en chaque sommet il y a la même configuration. Il y a 13 solides d'Archimède.
- Solides de Platon
Les solides de Platon sont les polyèdres réguliers. Il y en a cinq : le tétraèdre, l'octaèdre, l'icosaèdre, le cube et le dodécaèdre.
- Solides non polyédriques
Les solides non polyédriques sont les solides qui ne sont pas limités de toutes parts par des portions de plan.
- Somme de deux vecteurs
Si $\vec{u}$ est le vecteur $(u_x,u_y,u_z)$ et $\vec{v}$ le vecteur $(v_x,v_y,v_z)$ alors le vecteur somme est le vecteur $$\overrightarrow{u+v}=(u_x+v_x,u_y+v_y,u_z+v_z).$$
- Sphère
La sphère de centre $C=(x_c,y_c,z_c)$ et de rayon $r>0$ est l'ensemble de tous les points situés à la distance $r$ du point $C$.
- Tétraèdre
Le tétraèdre est un polyèdre régulier constitué de 4 faces, 4 sommets et 6 arêtes. Ses faces sont des triangles équilatéraux.
- Tore
Un tore est un solide engendré par la rotation d'un cercle autour d'une droite extérieure au cercle.
- Trapèze
Un trapèze est un quadrilatère qui a deux côtés opposés parallèles. Ces côtés parallèles sont appelés les bases du trapèze.
- Trapèze isocèle
Un trapèze dont les deux côtés non parallèles ont même longueur est un trapèze isocèle.
- Trapèze rectangle
Un trapèze qui possède un angle droit est un trapèze rectangle.
- Triangle
Un triangle est une figure géométrique plane qui a trois côtés, trois sommets et trois angles.
- Triangle équilatéral
Un triangle qui a 3 côtés égaux et 3 angles de même amplitude est dit équilatéral.
- Triangle isocèle
Un triangle isocèle a 2 côtés de même longueur et 2 angles de même amplitude.
- Triangle rectangle
Un triangle rectangle est un triangle ayant un angle droit.
- Triangles semblables
Deux triangles sont semblables si leurs angles ont deux à deux la même amplitude.
- Triplet pythagoricien
Un triplet pythagoricien est un triplet de nombres entiers représentant la longueur des côtés d'un triangle rectangle.
- Vecteur normal à un plan
Un vecteur normal à un plan est un vecteur qui est orthogonal à ce plan.
- Vecteurs colinéaires
Deux vecteurs sont colinéaires (ou parallèles) s'ils ont la même direction, c'est-à-dire s'il existe $\alpha\in\mathbb{R}$ tel que $\vec{u}=\alpha\vec{v}$.
- Vecteurs orthogonaux
Deux vecteurs sont orthogonaux s'ils forment un angle droit.