Théorèmes
- A01 - Propriété des proportions
-
Dans toute proportion, le produit des moyens est égal au produit des extrèmes, c'est-à-dire $\forall a,\, b,\, c,\, d\in\mathbb{R}_0$, on a $$ \frac{a}{b}=\frac{c}{d}\Leftrightarrow ad=bc. $$
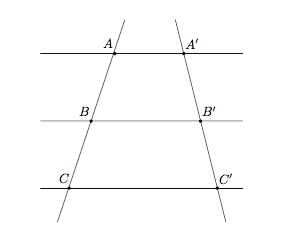
- A02 - Théorème de Thalès
-
Trois droites parallèles déterminent sur deux sécantes des segments homologues proportionnels.
Autrement dit, si trois droites parallèles rencontrent deux droites $d$ et $d'$, respectivement et dans cet ordre, en $A$, $B$, $C$ et $A'$, $B'$, $C'$, alors $$ \frac{\vert A'B'\vert}{\vert AB\vert}=\frac{\vert B'C'\vert}{\vert BC\vert}=\frac{\vert A'C'\vert}{\vert AC\vert}. $$
- B01 - Angle et cercle
-
Tout triangle inscrit dans un demi-cercle est un triangle rectangle.
Réciproquement, on peut inscrire tout triangle rectangle dans un demi-cercle dont le diamètre est l'hypoténuse du triangle.
- B02 - Angles alternes externes
-
Deux angles alternes externes ont même amplitude.
- B03 - Angles alternes internes
-
Deux angles alternes internes ont même amplitude.
- B04 - Angles correspondants
-
Deux angles correspondants ont même amplitude.
- B05 - Angles interceptant le même arc
-
Dans un cercle, des angles inscrits interceptant le même arc ont même amplitude.
- B06 - Angles opposés par le sommet
-
Deux angles opposés par le sommet ont même amplitude.
- B07 - Lien angle au centre-angle inscrit
-
Dans un cercle, l'amplitude de l'angle au centre vaut le double de l'amplitude de l'angle inscrit qui intercepte le même arc.
- C01 - Bissectrices d'un triangle
-
Les trois bissectrices d'un triangle se coupent en un même point. Ce point est le centre du cercle inscrit au triangle.
- C02 - Droite d'Euler
-
Dans tout triangle, le centre de gravité, l'orthocentre et le centre du cercle circonscrit sont alignés. La droite qui les contient est la droite d'Euler.
- C03 - Hauteurs d'un triangle
-
Les trois hauteurs d'un triangle se coupent en un même point. Ce point est l'orthocentre du triangle.
- C04 - Médianes d'un triangle
-
Les trois médianes d'un triangle se coupent en un même point. Ce point est le centre de gravité du triangle. Il est situé sur chaque médiane aux 2/3 de chacune d'elle à partir du sommet.
- C05 - Médiatrices d'un triangle
-
Les trois médiatrices d'un triangle se coupent en un même point. Ce point est le centre du cercle circonscrit au triangle.
- C06 - Milieu d'un côté d'un triangle
-
Dans tout triangle, la droite passant par le milieu d'un côté et parallèle à un autre côté coupe le troisième côté en son milieu.
Réciproquement, dans tout triangle, le segment joignant les milieux de deux des côtés est parallèle au troisième côté et sa longueur vaut la moitié de celle de ce troisième côté.
- C07 - Somme des angles d'un triangle
-
La somme des mesures des angles dans un triangle vaut toujours $180^\circ = \pi$ radians, c'est-à-dire $\alpha+ \beta+\gamma=180^\circ$.
- C08 - Théorème de Pythagore
-
Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
- C09 - Triangles isocèles
-
Dans un triangle isocèle,
- les angles à la base ont même amplitude
- la médiatrice de la base est égale à la bissectrice de l'angle opposé
- la médiatrice de la base est aussi médiane
- la médiatrice de la base est aussi hauteur
- C10 - Triangles rectangles
-
Les triangles rectangles possèdent les propriétés suivantes :
- Tout triangle inscrit dans un demi-cercle est rectangle.
- On peut inscrire tout triangle rectangle dans un demi-cercle dont le diamètre est l'hypoténuse du triangle.
- Dans un triangle rectangle, la longueur de la médiane relative à l'hypoténuse vaut la moitié de la longueur de l'hypoténuse.
- Dans un triangle rectangle, le carré de la longueur de la hauteur relative à l'hypoténuse est égal au produit des longueurs des segments qu'elle détermine sur l'hypoténuse.
- Dans un triangle rectangle, le carré de la longueur d'un côté de l'angle droit est égal au produit de la longueur de l'hypoténuse par la longueur de sa projection orthogonale sur l'hypoténuse.
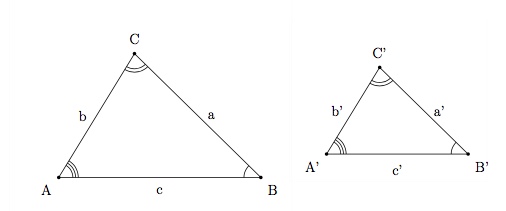
- C11 - Triangles semblables
-
Dans les triangles semblables, les côtés correspondants sont proportionnels, c'est-à-dire $$\displaystyle\frac{a}{a'}=\frac{b}{b'}=\frac{c}{c'}.$$
- D01 - Formules de trigonométrie
-
Formule fondamentale :
$\sin^2\alpha+\cos^2\alpha=1$
Formules de duplication :
$\sin (2\alpha) = 2 \sin \alpha \cos \alpha$
$\cos (2\alpha) = \cos ^2 \alpha - \sin ^2 \alpha = 1 - 2 \sin ^2\alpha = 2\cos ^2 \alpha - 1$
$\displaystyle \mbox{tg}(2\alpha) = \frac{2\, \mbox{tg }\alpha}{1- \mbox{tg}^2\alpha}$
Formules d'addition :
$\sin (\alpha + \beta) = \sin \alpha \cos\beta + \sin \beta \cos \alpha$
$\sin (\alpha -\beta) = \sin \alpha \cos\beta - \sin \beta \cos\alpha$
$\cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \beta \sin\alpha$
$\cos (\alpha - \beta) = \cos \alpha \cos\beta + \sin \beta \sin \alpha$
$\mbox{tg}(\alpha + \beta) = \dfrac{\mbox{tg }\alpha + \mbox{tg }\beta}{1- \mbox{tg }\alpha \cdot \mbox{tg }\beta}$
$\mbox{tg}(\alpha - \beta)= \dfrac{\mbox{tg }\alpha - \mbox{tg }\beta}{1+ \mbox{tg }\alpha \cdot \mbox{tg }\beta}$
Formules de Carnot :
$\sin ^ 2 \alpha = \dfrac{1 - \cos (2\alpha)}{2}$
$\cos ^ 2 \alpha = \dfrac{1 + \cos (2\alpha)}{2}$
$1+\mbox{tg}^2 \alpha = \dfrac{1}{\cos^2 \alpha}$
$1+\mbox{cotg}^2 \alpha =\dfrac{1}{\sin^2 \alpha}$
Formules de Simpson :
$\sin \alpha + \sin \beta = 2 \sin {(\frac{\alpha +\beta}{2})} \cos {(\frac{\alpha -\beta}{2})}$
$\sin \alpha - \sin \beta = 2 \sin {(\frac{\alpha -\beta}{2})} \cos {(\frac{\alpha +\beta}{2})}$
$\cos \alpha + \cos \beta = 2 \cos {(\frac{\alpha +\beta}{2})} \cos {(\frac{\alpha -\beta}{2})}$
$\cos \alpha - \cos \beta = -2 \sin {(\frac{\alpha -\beta}{2})} \sin{(\frac{\alpha +\beta}{2})}$
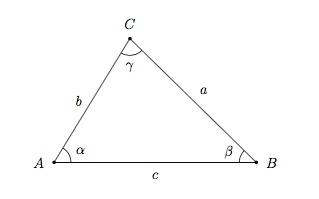
- D02 - Règle des sinus
-
Dans tout triangle, les longueurs des côtés sont proportionnelles aux sinus des angles opposés, c'est-à-dire si $a$, $b$ et $c$ sont les longueurs des côtés d'un triangle et $\alpha$, $\beta$ et $\gamma$ sont les angles opposés respectivement à ces côtés, on a
$$\frac{\sin \alpha}{a}=\frac{\sin \beta}{b}=\frac{\sin \gamma}{c}.$$
- D03 - Règles des cosinus
-
Dans tout triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés diminuée du double produit des longueurs de ces deux côtés par le cosinus de l'angle compris entre ces côtés, c'est-à-dire si $a$, $b$ et $c$ sont les longueurs des côtés d'un triangle et $\alpha$, $\beta$ et $\gamma$ sont les angles opposés respectivement à ces côtés, on a
$$ \begin{array}{l} a^2=b^2+c^2-2bc\cos{\alpha} \\ b^2=a^2+c^2-2ac\cos{\beta} \\ c^2=a^2+b^2-2ab\cos{\gamma} \end{array} $$
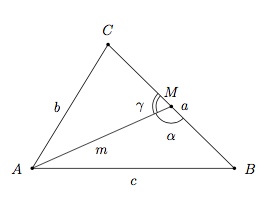
- D04 - Théorème de la médiane
-
La somme des carrés des longueurs de deux côtés d'un tiangle est égale à deux fois le carré de la longueur de la médiane relative au troisième côté plus deux fois le carré de la moitié de la longueur du troisième côté : $$b^2+c^2=2m^2+2\left(\dfrac{a}{2}\right)^2.$$
- E01 - Distance entre deux points
-
La distance entre les points $P_1= (x_1,y_1,z_1 )$ et $P_2= (x_2,y_2,z_2 )$ est le nombre réel positif $$ \begin{array}[t]{c} d(P_1,P_2)=\Vert\overrightarrow{P_1P_2}\Vert=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} \end{array} $$
- F01 - Composantes du produit vectoriel
-
Soit $\vec{u}=(u_x,u_y,u_z)$ et $\vec{v}=(v_x,v_y,v_z)$. Les composantes du vecteur $\vec{u}\times\vec{v}$ sont données par
$$\vec{u}\times\vec{v}=(u_yv_z-u_zv_y,u_zv_x-u_xv_z, u_xv_y-u_yv_x).$$
- F02 - Inégalité de Cauchy-Schwartz
-
Si $\vec{u}$ et $\vec{v}$ sont deux vecteurs alors $|\vec{u}\odot\vec{v}|\le \|\vec{u}\|\|\vec{v}\|$.
- F03 - Inégalité triangulaire
-
Si $\vec{u}$ et $\vec{v}$ sont deux vecteurs alors $\|\vec{u}+\vec{v}\|\le\|\vec{u}\|+\|\vec{v}\|$.
- F04 - Longueur du produit vectoriel
-
La longueur $\|\vec{u}\times\vec{v}\|$ est l'aire du parallélogramme construit sur les vecteurs $\vec{u}$ et $\vec{v}$.
- F05 - Moment d'une force
-
Le moment d'une force $\overrightarrow{F}$ appliquée en un point $A$, par rapport à un point $P$ est le produit vectoriel entre le vecteur position de cette force par rapport au point de référence et le vecteur force lui-même, soit $$\overrightarrow{M}=\overrightarrow{PA}\times\overrightarrow{F}.$$
- F06 - Produit mixte
-
Le produit mixte de 3 vecteurs $\vec u$, $\vec v $ et $\vec w $ est le nombre réel $| (\vec u \times \vec v) \odot \vec w |$. Il donne le volume du parallélipipède construit sur les 3 vecteurs, où $\vec u$ et $\vec v$ forment la base du parallélipipède.
- F07 - Produit scalaire
-
Si $\theta$ désigne l'angle entre les deux vecteurs non nuls $\vec{u}$ et $\vec{v}$, alors $$\vec{u}\odot\vec{v}=\|\vec{u}\|\|\vec{v}\|\cos\theta.$$
- F08 - Travail d'un force
-
Le travail $W$ d'une force d'intensité constante $\overrightarrow{F}$ appliquée à un point en mouvement le long d'un vecteur $\overrightarrow{d}$ est $W=\overrightarrow{F}\odot\overrightarrow{d}$.
- G01 - Equation d'un cercle
-
L'équation du cercle centré en $(x_c,y_c)$ et de rayon $r$ est donnée par $(x-x_c)^2+(y-y_c)^2=r^2.$
- G02 - Equation d'une droite de pente donnée et passant par un point donné
-
L'équation cartésienne de la droite de pente $m$ passant par le point $P_1=(x_{1},y_{1})$ est donnée par $y-y_1 = m (x-x_1).$
- G03 - Equation d'une droite passant par deux points donnés
-
L'équation cartésienne de la droite passant par les points $P_1=(x_{1},y_{1})$ et $P_2=(x_2,y_2)$ est donnée par $y-y_1 = \dfrac{y_2-y_1}{x_2-x_1} (x-x_1).$
- H01 - Conditions d'orthogonalité
-
Orthogonalité de deux droites : Soit $\Delta_1$ de direction $\vec u$ et $\Delta_2$ de direction $\vec v$. Les droites $\Delta_1$ et $\Delta_2$ sont orthogonales si et seulement si les vecteurs directeurs $\vec u=(u_x,u_y,u_z)$ et $\vec v=(v_x,v_y,v_z)$ sont orthogonaux.
Orthogonalité de deux plans : Soit $\Pi_1$ le plan d'équation $n_x x+n_y y+n_z z+d_1=0$ et $\Pi_2$ le plan d'équation $m_x x+m_y y+m_z z+d_2=0$. Les plans $\Pi_1$ et $\Pi_2$ sont orthogonaux si et seulement si les vecteurs normaux $\vec n=(n_x,n_y,n_z)$ et $\vec m=(m_x,m_y,m_z)$ sont orthogonaux.
Orthogonalité d'un plan et d'une droite : Soit $\Delta$ la droite de direction $\vec u$ et $\Pi$ le plan d'équation $n_x x+n_y y+n_z z+d=0$. Le plan $\Pi$ est orthogonal à la droite $\Delta$ si et seulement si le vecteur $\vec u$ est proportionnel au vecteur $\vec n=(n_x,n_y,n_z)$.
- H02 - Conditions de parallélisme
-
Parallélisme de deux droites : Soit $\Delta_1$ de direction $\vec u$ et $\Delta_2$ de direction $\vec v$. Les droites $\Delta_1$ et $\Delta_2$ sont parallèles si et seulement si les vecteurs directeurs $\vec u$ et $\vec v$ sont proportionnels.
Parallélisme de deux plans : Soit $\Pi_1$ le plan d'équation $n_x x+n_y y+n_z z+d_1=0$ et $\Pi_2$ le plan d'équation $m_x x+m_y y+m_z z+d_2=0$. Les plans $\Pi_1$ et $\Pi_2$ sont parallèles si et seulement si les vecteurs normaux $\vec n=(n_x,n_y,n_z)$ et $\vec m=(m_x,m_y,m_z)$ sont proportionnels.
Parallélisme d'un plan et d'une droite : Soit $\Delta$ la droite de direction $\vec u$ et $\Pi$ le plan d'équation $n_x x+n_y y+n_z z+d=0$. Le plan $\Pi$ est parallèle à la droite $\Delta$ si et seulement si le vecteur $\vec u$ est orthogonal au vecteur $\vec n=(n_x,n_y,n_z)$.
- H03 - Distance
-
Distance entre deux points : Soit $P_1 = (x_1,y_1,z_1 )$ et $P_2 = (x_2,y_2,z_2 )$ deux points distincts de $\mathbb{R}^3$. La distance entre les points $P_1$ et $P_2$ s'obtient en calculant la norme du vecteur $\overrightarrow{P_1P_2}$ : $$d(P_1,P_2)=\Vert\overrightarrow{P_1P_2}\Vert=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$$
Distance d'un point à un plan : La distance du point $P_1 = (x_1,y_1,z_1 )$ au plan $\Pi$ décrit par l'équation $n_x x + n_y y + n_z z + d=0$ est donnée par le nombre réel positif $$d(P_1,\Pi) = \dfrac{|n_x x_1 + n_y y_1 + n_z z_1 +d|}{\sqrt{n^2_x +n^2_y + n^2_z }}.$$
Distance d'un point à une droite : Pour trouver la distance du point $P_1$ à la droite $\Delta$, on mène par $P_1 $ un plan $\Pi$ perpendiculaire à $\Delta$ et on cherche le point d'intersection $Q$ entre $\Pi$ et $\Delta$. La distance entre $P_1$ et $\Delta$ est $\| \overrightarrow{P_1 Q} \|$.
Distance entre deux plans : Pour déterminer la distance entre deux plans parallèles, il suffit de trouver les coordonnées d'un point d'un des plans et de calculer la distance de ce point à l'autre plan.
Distance entre deux droites : Pour déterminer la distance entre deux droites parallèles, il suffit de trouver les coordonnées d'un point d'une des droites et de calculer la distance de ce point à l'autre droite. Pour déterminer la distance entre deux droites gauches $\Delta_1 $ passant par $P_1 $ et de direction $\vec u$ et $\Delta_2 $ passant par $P_2 $ et de direction $\vec v$, on écrit l'équation du plan $\Pi$ passant par $P_2 $ et parallèle à la fois à $\vec u$ et à $\vec v$. La distance entre les deux droites est celle de $P_1 $ à $\Pi$.
Distance d'une droite à un plan : Pour déterminer la distance entre une droite et un plan parallèle, il suffit de trouver les coordonnées d'un point de la droite et de calculer la distance entre ce point et le plan.
- H04 - Equation d'un plan passant par un point donné et orthogonal à un vecteur fixé
-
L'équation du plan $\Pi$ passant par $P_0 = (x_0,y_0,z_0 )$ et orthogonal au vecteur $\vec n=(n_x,n_y,n_z)$ est donnée par $$ n_x x + n_y y + n_z z = n_x x_0 + n_y y_0 + n_z z_0. $$
- H05 - Equation d'une droite passant par un point donné et parallèle à un vecteur fixé
-
L'équation de la droite $\Delta$ passant par $P_0 = (x_0,y_0,z_0 ) $ et parallèle au vecteur $\vec u=(u_x,u_y,u_z)$ est donnée par $$ \left\{\begin{array}{c} \displaystyle\frac{x-x_0}{u_x} = \frac{y-y_0 }{u_y}\\[2mm] \displaystyle\frac{y-y_0}{u_y} = \frac{z-z_0} {u_z} \end{array}\right. $$ si $u_xu_yu_z\neq 0$.
- H06 - Equation de la sphère
-
La sphère centrée en $(x_c,y_c,z_c)$ et de rayon $r$ a pour équation $(x-x_c)^2+(y-y_c)^2+(z-z_c)^2=r^2$.
- J01 - Polygones réguliers
-
Tout polygone régulier admet un axe de symétrie.
Tout polygone régulier peut être inscrit dans un cercle.
- J02 - Formules pour la surface d'un triangle
-
La surface $S$ du triangle de côtés $a$, $b$, $c$ est donnée par
- $S=\dfrac{ch}{2}$ où $h$ est la hauteur perpendiculaire à $c$;
- $S=\dfrac{bc\sin{\alpha}}{2}$ où $\alpha$ est l'angle entre les côtés $b$ et $c$;
- $S=\dfrac{r(a+b+c)}{2}=\dfrac{rP}{2}$ où $P$ est le périmètre et $r$ est le rayon du cercle inscrit;
- $S=\dfrac{\sqrt{P(P-2a)(P-2b)(P-2c)}}{4}$ où $P$ est le périmètre (Formule de Héron);
- $S=\dfrac{abc}{4R}$ où $R$ est le rayon du cercle circonscrit.
- J03 - Propriété du trapèze
-
Dans un trapèze, la droite qui joint les milieux des deux côtés non parallèles est parallèle aux bases.
- J04 - Propriétés du carré
-
Dans un carré,
- les diagonales sont perpendiculaires, se coupent en leur milieu et ont même longueur;
- les médianes sont perpendiculaires, se coupent en leur milieu et ont même longueur;
- les médianes sont parallèles aux côtés;
- les diagonales et les médianes se coupent en un même point.
- J05 - Propriétés du losange
-
Dans un losange,
- les diagonales sont perpendiculaires et se coupent en leur milieu;
- les médianes ont même longueur et se coupent en leur milieu;
- les médianes sont parallèles aux côtés;
- les diagonales et les médianes se coupent en un même point.
- J06 - Propriétés du parallélogramme
-
Dans un parallélogramme,
- les diagonales se coupent en leur milieu;
- les médianes se coupent en leur milieu;
- les médianes sont parallèles aux côtés;
- les diagonales et les médianes se coupent en un même point.
- J07 - Propriétés du rectangle
-
Dans un rectangle,
- les diagonales ont même longueur et se coupent en leur milieu;
- les médianes sont perpendiculaires et se coupent en leur milieu;
- les médianes sont parallèles aux côtés;
- les diagonales et les médianes se coupent en un même point, centre du cercle circonscrit au rectangle.
- J08 - Somme des angles d'un polygone
-
La somme des mesures des angles d'un polygône à $n$ côtés vaut $(n-2)\times 180^{\circ}$.
- K01 - Principe de Cavalieri
-
Soit deux solides compris entre deux plans parallèles. Supposons que chaque plan parallèle aux premiers coupe les deux solides en des surfaces de même aire. Alors, dans ces conditions, les deux solides ont même volume.
- K02 - Théorème d'Euler
-
Dans tout polyèdre convexe, régulier ou non, on a $$S+F=A+2,$$ où $S$, $F$ et $A$ sont respectivement le nombre de sommets, de faces et d'arêtes du polyèdre.