LBARC 1143 Mathématique Géométrie Anciens Examens Examen de Janvier 2016

Examen de Janvier 2016

Pour vous tester, essayez de résoudre cet ancien examen.

Imprimer en PDF
1

On considère le triangle $ABC$ de côtés $a$, $b$ et $c$.

  1. Définissez le cercle circonscrit à ce triangle.

    Le cercle circonscrit au triangle est le cercle dont le centre est l'intersection des médiatrices du triangle et qui passe par ses 3 sommets.

  2. Démontrez que la surface de ce triangle est donnée par $$ S=\dfrac{abc}{4R} $$ où $R$ est le rayon du cercle circonscrit au triangle.

    Soit $O$ le centre du cercle circonscrit et $E$ l'intersection de la droite $OC$ avec le cercle.

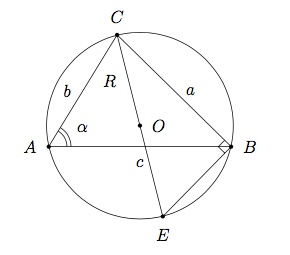
    Le triangle $BEC$ est rectangle en $B$ car il est inscrit dans un demi-cercle.

    De plus, $\widehat{E}=\widehat{A}$ car ils sous-tendent le même arc $BC$.

    On en déduit que $\widehat{E}=\alpha$ et $\sin{\alpha}=\dfrac{a}{2R}$.

    Or $$ S=\dfrac{bc\sin\alpha}{2} $$ et donc $$ S=\dfrac{bc}{2}\cdot\dfrac{a}{2R}=\dfrac{abc}{4R} $$ où $R$ est le rayon du cercle circonscrit.
2

On voudrait fabriquer un cône en papier pour mettre des bonbons. Pour cela, on découpe un secteur dans un disque de rayon $15$ cm et on colle $OA$ à $OB$. Déterminez l'angle $\alpha$ pour avoir un cône de $12$ cm de profondeur.

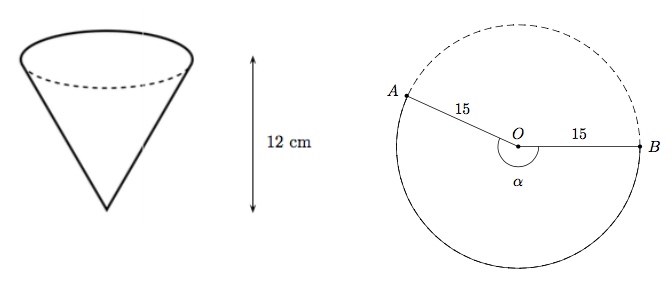
Soit $r$ le rayon du cône. On calcule $$ r^2+12^2=15^2, $$ $$ r^2=225-144=81, $$ $$ r=9. $$ Il faut trouver $\alpha$ pour que $$ 2\pi\, r=15\alpha, $$ $$ 18\pi=15\alpha, $$ $$ \alpha=\dfrac{18}{15}\pi=\dfrac{6}{5}\pi. $$

3

On considère les deux cercles $$ C_1\, :\, x^2+y^2+4x+4y-17=0, $$ $$ C_2\, :\, x^2+y^2-8x+10y+31=0. $$

  1. Donnez le centre et le rayon de $C_1$.

    L'équation du cercle $C_1$ peut s'écrire $$ x^2+4x+4+y^2+4y+4=17+4+4 $$ ou encore $$ (x+2)^2+(y+2)^2=25. $$ Le centre est donc $(-2,-2)$ et le rayon vaut $5$.

  2. Donnez le centre et le rayon de $C_2$.

    L'équation du cercle $C_2$ peut s'écrire $$ x^2-8x+16+y^2+10y+25=-31+16+25 $$ ou encore $$ (x-4)^2+(y+5)^2=10. $$ Le centre est donc $(4,-5)$ et le rayon vaut $\sqrt{10}$.

  3. Déterminez l'équation de la droite $AB$ où $A$ et $B$ sont les points d'intersection des cercles $C_1$ et $C_2$.

    Pour trouver l'intersection des deux cercles il faut résoudre l'équation $$ x^2+y^2+4x+4y-17=x^2+y^2-8x+10y+31. $$ On trouve $12x-6y=48$ ou encore $y=2x-8$.

    La droite $AB$ est donc une droite de pente $m=2$ qui a pour équation $y=2x-8$.

  4. Montrez que la droite reliant les deux centres est perpediculaire à la droite $AB$.

    La pente de la droite reliant les deux centre vaut $$ m'=\dfrac{-5+2}{4+2}=-\dfrac{3}{6}=-\dfrac{1}{2}. $$ Vu que $m\cdot m'=2\cdot\dfrac{-1}{2}=-1$, on en déduit que les deux droites sont perpendiculaires.
4

On considère le plan $\Pi\, :\, x+y+2z=3$ et les droites

$$ \Delta_1\, :\, \left\{ \begin{array}{l} 5x+3y+15=0\\ y+5z-20=0 \end{array} \right. $$ et $$ \Delta_2\, :\, \left\{ \begin{array}{l} x=2-2k\\ y=k\\ z=5-2k \end{array} \right. $$ avec $k\in\mathbb{R}$.

  1. Donnez un vecteur normal au plan $\Pi$.

    Le vecteur $\vec{n}=(1,1,2)$ est un vecteur normal au plan $\Pi$.

  2. Donnez un vecteur directeur et un point de la droite $\Delta_1$.

    On calcule $$ (5,3,0)\times (0,1,5)=(15,-25,5)=5(3,-5,1). $$ Le vecteur $\vec{v_1}=(3,-5,1)$ est donc un vecteur directeur de la droite $\Delta_1$ et $P_1=(-3,0,4)$ est un point de cette droite.

  3. Donnez un vecteur directeur et un point de la droite $\Delta_2$.

    Le vecteur $\vec{v_2}=(-2,1,-2)$ est un vecteur directeur de la droite $\Delta_2$ et $P_2=(2,0,5)$ est un point de cette droite.

  4. Déterminez si les droites $\Delta_1$ et $\Delta_2$ sont parallèles ou sécantes avec le plan $\Pi$.

    Si la droite est parallèle au plan, précisez la distance entre la droite et le plan.

    Si la droite et le plan sont sécants, donnez leur point d'intersection.

    Vu que $\vec{v_1}\neq k\vec{n}$ et $\vec{v_2}\neq k\vec{n}$, les droites ne sont pas orthogonales à $\Pi$.

    Puisque $\vec{v_1}\odot\vec{n}=3-5+2=0$, la droite $\Delta_1$ est parallèle à $\Pi$.

    Puisque $\vec{v_2}\odot\vec{n}=-2+1-4\neq 0$, la droite $\Delta_2$ n'est pas parallèle à $\Pi$. Elle est donc sécante à $\Pi$.

    Calculons la distance entre $\Delta_1$ et $\Pi$ : $$ \mbox{dist}(\Delta_1,\Pi)=\mbox{dist}(P_1,\Pi)=\dfrac{|-3+0+8-3|}{\sqrt{1+1+4}}=\dfrac{2}{\sqrt{6}}=\dfrac{\sqrt{6}}{3}. $$ Pour trouver le point d'intersection entre $\Delta_2$ et $\Pi$, il faut résoudre le système $$ \left\{ \begin{array}{l} x+y+2z=3\\ x=2-2k\\ y=k\\ z=5-2k \end{array} \right. $$ On trouve $2-2k+k+10-4k=3$ et donc $k=\frac{9}{5}$.

    On en déduit $x=-\frac{8}{5}$, $y=\frac{9}{5}$ et $z=\frac{7}{5}$. Le point d'intersection est donc le point $(-\frac{8}{5},\frac{9}{5},\frac{7}{5})$.
5

Les propositions suivantes sont-elles vraies ou fausses ? Répondez par V ou F dans la case à la fin de la phrase, sans justifier. Une mauvaise réponse entraînera l'annulation d'une bonne réponse. Vous pouvez vous abstenir sans être pénalisé.

  1. En topologie, une paire de ciseaux est une surface de genre 2.

    Vrai.

  2. Si $\vec{u}$, $\vec{v}$ et $\vec{w}$ sont 3 vecteurs de $\mathbb{R}^3$, on a toujours $(\vec{u}\times\vec{v})\times\vec{w}=\vec{u}\times(\vec{v}\times\vec{w})$.

    Faux.

    Le produit vectoriel n'est pas associatif.

  3. Pour tout $x\in\mathbb{R}$, on a $\sin{x}=-\cos{(\frac{\pi}{2}+x)}$.

    Vrai.

  4. Le point $P=(2,-2\sqrt{3})$ est à distance $4$ de l'origine.

    Vrai.

  5. Le point $M=(1,4,1)$ est le milieu du segment $AB$, où $A=(2,-2,0)$ et $B=(4,6,2)$.

    Faux.

    Le milieu du segment $AB$ et le point $M=(3,2,1)$.
6

Ecrivez la réponse correcte dans la case à la fin de la phrase sans justifier.

  1. Soit $A=(-1,1)$, $B=(2,1)$ et $C=(-2,3)$. Déterminez les coordonnées du point $M$ tel que $\overrightarrow{AM}=2\overrightarrow{BC}$.

    Soit $M=(a,b)$. Il faut que $\overrightarrow{AM}=2\overrightarrow{BC}$, c'est-à-dire $(a+1,b-1)=2(-4,2)$. On en déduit $M=(a,b)=(-9,5)$.

  2. Que deviennent les coordonnées du point $P=(5,0,-3)$ quand on translate l'origine du repère vers le point $(-3,2,-4)$ ?

    Les équations de changement de repère sont $$ \left\{ \begin{array}{l} x=-3+x'\\ y=2+y'\\ z=-4+z' \end{array} \right. $$ et donc $(x',y',z')=(x+3,y-2,z+4)=(5+3,0-2,-3+4)=(8,-2,1)$.

  3. Déterminez $m\in\mathbb{R}$ pour que les vecteurs $\vec{u}=(m,0,-8)$ et $\vec{v}=(-1,3,-5)$ soient orthogonaux.

    Les vecteurs $\vec{u}=(m,0,-8)$ et $\vec{v}=(-1,3,-5)$ sont orthogonaux si et seulement si $\vec{u}\odot\vec{v}=0$, c'est-à-dire si et seulement si $-m+40=0$ donc si $m=40$.

  4. Donnez l'équation du plan médiateur du segment $AB$ où $A=(2,-2,0)$ et $B=(4,6,2)$.

    Le plan médiateur est orthogonal au segment et passe par son milieu.

    Un vecteur normal au plan est donc $\vec{n}=\overrightarrow{AB}=(2,8,2)$ et il passe par le milieu du segment, à savoir le point $M=(3,2,1)$.

    L'équation de ce plan est donc $x+4y+z=12$.

  5. Si $\vec{u}=(-1,-3,-2)$ et $\vec{v}=(2,2,-4)$, calculez $\vec{u}\times\vec{v}$.

    $(16,-8,4)$