Examen de Janvier 2017
Pour vous tester, essayez de résoudre cet ancien examen.
Définissez le produit vectoriel de deux vecteurs dans $\mathbb{R}^3$.
Le produit vectoriel de 2 vecteurs $\vec{u}$ et $\vec{v}$ est le vecteur $\vec{u}\times\vec{v}$ tel que
$\bullet\, \, \vec{u}\times\vec{v}$ est orthogonal à $\vec{u}$ et à $\vec{v}$,
$\bullet\, \, \Vert\vec{u}\times\vec{v}\Vert=\Vert\vec{u}\Vert\cdot\Vert\vec{v}\Vert\cdot\vert\sin{\theta}\vert$,
$\bullet\, \, \vec{u},\, \vec{v}\mbox{ et } \vec{u}\times\vec{v}$ pris dans cet ordre forment un repère droit.
On vous demande de concevoir un pont basculant qui a une longueur de 50 mètres lorsqu'il est abaissé au dessus d'une rivière. Les deux parties de ce pont ont même longueur, sont fixées à leur extrémité et peuvent être relevées d'un angle de maximum $45$ degrés. Sachant que le niveau de l'eau est à 5 mètres sous le pont abaissé,
-
calculez la distance $d$ entre l'extrémité d'une partie du pont et l'eau lorsque le pont est entièrement levé;
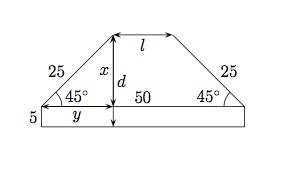
La situation peut être représentée par le schéma ci-dessus.
On a $d=x+5$ et $\sin{45^{\circ}}=\dfrac{x}{25}$ d'où $x=\dfrac{25\sqrt{2}}{2}$.
-
calculez la distance entre les extrémités des deux parties du pont lorsque celui-ci est entièrement levé.
La situation peut être représentée par le schéma ci-dessus.
On a $l=50-2y$ et $\cos{45^{\circ}}=\dfrac{y}{25}$ d'où $y=\dfrac{25\sqrt{2}}{2}$.
On en déduit $l=50-25\sqrt{2}$ mètres.
-
Représentez la situation lorsque le pont est entièrement levé.
Démontrez que la surface $S$ du triangle de côtés $a$, $b$, $c$ est donnée par $$ S=\dfrac{abc}{4R} $$ où $R$ est le rayon du cercle circonscrit au triangle.
Soit $O$ le centre du cercle circonscrit et $E$ l'intersection de la droite $OC$ avec le cercle.
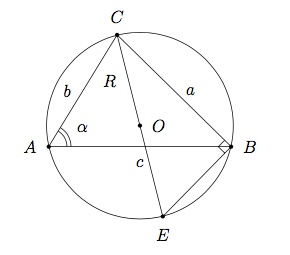
Le triangle $BEC$ est rectangle en $B$ car il est inscrit dans un demi-cercle.
De plus, $\widehat{E}=\widehat{A}$ car ils sous-tendent le même arc $BC$.
On en déduit que $\widehat{E}=\alpha$ et $\sin{\alpha}=\dfrac{a}{2R}$.
Or $$ S=\dfrac{bc\sin\alpha}{2} $$ et donc $$ S=\dfrac{bc}{2}\cdot\dfrac{a}{2R}=\dfrac{abc}{4R} $$ où $R$ est le rayon du cercle circonscrit.
On considère la pile suivante. Calculez son volume ainsi que l'aire d'une étiquette qui ferait tout le tour de la pile.

La base de la pile est constituée d'un rectangle de $4$ cm sur $1$ cm et d'un disque de diamètre $1$ cm. Sa hauteur vaut $6$ cm. Le volume de la pile est donc $$ V=(4\cdot 1+\pi\cdot(0,5)^2)\cdot 6=24+\dfrac{3\pi}{2}\mbox{ cm}^3. $$ Le périmètre de la base vaut $4+4+2\cdot\pi\cdot (0,5)=8+\pi$ cm et donc la surface de l'étiquette est $$ S=(8+\pi)\cdot 6=48+6\pi\mbox{ cm}^2. $$
Enoncez le Théorème de Thalès.
Théorème de Thalès : Trois droites parallèles déterminent sur deux sécantes des segments homologues proportionnels.
On considère le triangle $ABC$ représenté ci-dessous où $AC$ est de longueur $3$ et $DF$ de longueur $1$. Calculez la surface $S$ du triangle $FEB$.
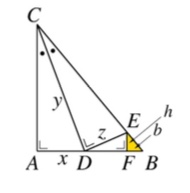
Pour cela,
-
déterminez deux triangles semblables au triangle $ADC$. Justifiez et écrivez les égalités correspondantes;
Les triangles $ADC$ et $DEC$ sont semblables car ils ont un angle droite et le même angle en $C$. On a donc $$ \dfrac{|AC|}{|DC|}=\dfrac{|AD|}{|DE|}=\dfrac{|CD|}{|CE|}\hspace{1cm}\mbox{ ou encore }\hspace{1cm}\dfrac{3}{y}=\dfrac{x}{z}=\dfrac{y}{|CE|}. $$ Les triangles $ADC$ et $DEF$ sont semblables car ils ont un angle droite et $\widehat{ACD}+\widehat{CDA}=90^{\circ}$, $\widehat{EDF}+\widehat{CDA}=90^{\circ}$ donc $\widehat{ACD}=\widehat{EDF}$. On a donc $$ \dfrac{|AD|}{|EF|}=\dfrac{|AC|}{|DF|}=\dfrac{|CD|}{|DE|}\hspace{1cm}\mbox{ ou encore }\hspace{1cm}\dfrac{x}{h}=\dfrac{3}{1}=\dfrac{y}{z}. $$
-
déduisez-en la longueur $x$;
On déduit des inégalités ci-dessus que $\dfrac{z}{y}=\dfrac{x}{3}\mbox{ et }\dfrac{z}{y}=\dfrac{1}{3}$ donc $x=1$.
-
déterminez $h$ et $b$ et déduisez-en la surface $S$.
On déduit des inégalités ci-dessus que $\dfrac{h}{x}=\dfrac{1}{3}$ donc $h=\dfrac{1}{3}$.
De plus, par Thalès, on a $$ \dfrac{|AC|}{|AB|}=\dfrac{|EF|}{|FB|}\hspace{1cm}\mbox{ ou encore }\hspace{1cm}\dfrac{3}{x+1+b}=\dfrac{h}{b}. $$ On en déduit $3b=h(x+1+b)=\dfrac{1}{3}(2+b)$ et donc $b=\dfrac{1}{4}$.
Finalement la surface demandée est $$ S=\dfrac{b\cdot h}{2}=\dfrac{1}{24}. $$
On considère la sphère ayant pour équation $$ x^2+y^2+z^2-2x+4y-6z=2. $$
-
Déterminez le centre et le rayon de cette sphère.
En complétant les carrés, on obtient $$ \begin{array}{c} x^2-2x+1+y^2+4y+4+z^2-6z+9=2+1+4+9\\ (x-1)^2+(y+2)^2+(z-3)^2=16 \end{array} $$ Il s'agit donc de la sphère de centre $C=(1,-2,3)$ et de rayon $r=\sqrt{16}=4$.
-
Déterminez l'intersection de la sphère avec le plan $OXY$. De quelle forme géométrique s'agit-il ? Précisez son équation et ses caractéristiques.
Pour trouver l'intersection de la sphère avec le plan $OXY$ on résoud le système $$ \left\{ \begin{array}{l} x^2+y^2+z^2-2x+4y-6z=2\\ z=0 \end{array} \right. $$ On trouve $$ \begin{array}{c} x^2-2x+1+y^2+4y+4=2+1+4\\ (x-1)^2+(y+2)^2=7 \end{array} $$ Il s'agit du cercle de centre $(1,-2)$ et de rayon $\sqrt{7}$ dans le plan $z=0$.
Soit $P=(-1,2,1)$ et $\Pi\, :\, x-y+2z-5=0$.
-
Déterminez un point et un vecteur normal au plan $\Pi$.
Le vecteur $\vec{n}=(1,-1,2)$ est un vecteur normal au plan $\Pi$ et $X=(5,0,0)$ est un point de ce plan.
-
Déterminez le point $Q$, projection orthogonale de $P$ sur $\Pi$.
Soit $Q=(a,b,c)$. Puisque $\overrightarrow{PQ}\parallel\vec{n}$, on a $$ (a+1,b-2,c-1)=k(1,-1,2) $$ pour un certain $k\in\mathbb{R}$ et donc $Q=(a,b,c)=(-1+k,2-k,1+2k)$.
De plus, $Q\in\Pi$ et donc $a-b+2c=5$ ou $-1+k-2+k+2+4k=5$, ce qui implique $k=1$.
Finalement $Q=(a,b,c)=(-1+k,2-k,1+2k)=(0,1,3)$.
-
Déterminez le point $R$, symétrique du point $P$ par rapport à $\Pi$.
Soit $R=(a,b,c)$. On a $\overrightarrow{PQ}=\overrightarrow{QR}$ et donc $(1,-1,2)=(a,b-1,c-3)$, d'où $R=(a,b,c)=(1,0,5)$.
-
Déterminez la distance entre le point $P$ et le plan $\Pi$.
La distance entre le point $P$ et le plan $\Pi$ est donnée par $$ \mbox{dist}(P,\Pi)=\Vert\overrightarrow{PQ}\Vert=\Vert(1,-1,2)\Vert=\sqrt{1+1+4}=\sqrt{6} $$ ou encore par la formule $$ \mbox{dist}(P,\Pi)=\dfrac{|-1-2+2-5|}{\sqrt{1+1+4}}=\dfrac{6}{\sqrt{6}}=\sqrt{6}. $$
Les propositions suivantes sont-elles vraies ou fausses ? Répondez par V ou F dans la case à la fin de la phrase, sans justifier. Une mauvaise réponse entraînera l'annulation d'une bonne réponse. Vous pouvez vous abstenir sans être pénalisé.
-
Pour tout $x\in\mathbb{R}$, on a $\cos{(2x)}=2\, \sin{x}\, \cos{x}$.
Faux.
On a $\cos{(2x)}=\cos^2{x}-\sin^2{x}$.
-
Le point $P=(2,-2\sqrt{3})$ se trouve à distance $16$ de l'origine.
Faux.
La distance entre le point $P=(2,-2\sqrt{3})$ et l'origine est donnée par $$ \sqrt{2^2+(-2\sqrt{3})^2}=\sqrt{4+12}=\sqrt{16}=4. $$
-
Le nombre $\vec{a}\odot\vec{b}$ représente l'aire du parallélogramme construit sur les vecteurs $\vec{a}$ et $\vec{b}$.
Faux.
C'est le nombre $||\vec{a}\times\vec{b}||$ qui représente l'aire du parallélogramme construit sur $\vec{a}$ et $\vec{b}$.
-
La résultante des forces $\overrightarrow{F_1}$ et $\overrightarrow{F_2}$ est obtenue en additionnant ces deux forces.
Vrai.
-
La pente de la droite $3x-2y+4=0$ vaut $3$.
Faux.
La pente de la droite est obtenue en isolant $y$ dans l'équation de la droite : $y=\frac{3}{2}x+2$. La pente vaut donc $\frac{3}{2}$.
Ecrivez la réponse correcte dans la case à la fin de la phrase sans justifier.
-
Soit $A=(-1,1)$ et $B=(2,1)$. Déterminez les coordonnées du vecteur $\overrightarrow{AB}$.
On a $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=(2,1)-(-1,1)=(3,0)$.
-
Déterminez l'équation de la droite passant par les points $(1,2)$ et $(4,4)$.
L'équation de cette droite est $$ y-2=\dfrac{4-2}{4-1}(x-1) $$ c'est-à-dire $y=\dfrac{2}{3}x+\dfrac{4}{3}$.
-
Déterminez l'angle d'un polygone régulier à $9$ côtés.
On décompose le polygone en triangles puis on calcule dans un triangle $\alpha+\alpha+\frac{2\pi}{9}=\pi$. Donc $\alpha=\frac{7\pi}{18}$ et l'angle du polygone vaut $2\alpha=\frac{7\pi}{9}$.
-
Donnez l'équation du plan médiateur du segment $AB$ où $A=(3,-3,0)$ et $B=(5,7,4)$.
Le plan médiateur est orthogonal au segment et passe par son milieu.
Un vecteur normal au plan est donc $\vec{n}=\overrightarrow{AB}=(2,10,4)$ et il passe par le milieu du segment, à savoir le point $M=(4,2,2)$.
L'équation de ce plan est donc $x+5y+2z=18$.
-
Par combien est multiplié le volume d'un cône circulaire si on triple son rayon et on divise par 2 sa hauteur ?
Le volume de l'ancien cône est $V=\frac{1}{3}\, \pi\, r^2\, h$.
Le volume du nouveau cône est $V'=\frac{1}{3}\, \pi\, (3r)^2\, \frac{h}{2}=\frac{1}{3}\, \pi\, 9\, r^2\, \frac{h}{2}=\frac{9}{2}V$.
Le volume est donc multiplié par $\frac{9}{2}$.