Examen de Janvier 2018
Pour vous tester, essayez de résoudre cet ancien examen.
Soit $\vec{u}$ et $\vec{v}$ deux vecteurs de $\mathbb{R}^3$.
-
Définissez le produit vectoriel des vecteurs $\vec{u}$ et $\vec{v}$.
Le produit vectoriel de 2 vecteurs $\vec{u}$ et $\vec{v}$ est le vecteur $\vec{u}\times\vec{v}$ tel que
$\bullet\, \, \vec{u}\times\vec{v}$ est orthogonal à $\vec{u}$ et à $\vec{v}$,
$\bullet\, \, \Vert\vec{u}\times\vec{v}\Vert=\Vert\vec{u}\Vert\cdot\Vert\vec{v}\Vert\cdot\vert\sin{\theta}\vert$,
$\bullet\, \, \vec{u},\, \vec{v}\mbox{ et } \vec{u}\times\vec{v}$ pris dans cet ordre forment un repère droit.
-
Démontrez que l'aire du parallélogramme construit sur les vecteurs $\vec{u}$ et $\vec{v}$ est donnée par $\Vert\vec{u}\times\vec{v}\Vert$.
Plaçons l'origine des vecteurs $\vec{u}$ et $\vec{v}$ au même point $O$, $\vec u=\overrightarrow{OU}$ et $\vec v=\overrightarrow{OV}$. Soit $P$ la projection orthogonale de $\vec v$ sur $\vec u$. L'aire du parallélogramme est donnée par
$A=\Vert\overrightarrow{OU}\Vert\cdot\Vert\overrightarrow{VP\Vert}=\Vert\vec u\Vert\cdot\Vert\vec v\Vert\cdot\sin{\alpha}=\Vert\vec u\times\vec v\Vert.$
Une tour est protégée par un large fossé. Un observateur au point $A$ voit le sommet de la tour sous un angle de $45^\circ$. En reculant de $10$ mètres, il se trouve en $B$ et voit le sommet de la tour sous un angle de $30^\circ$. Déterminez la hauteur de la tour ainsi que la largeur du fossé.
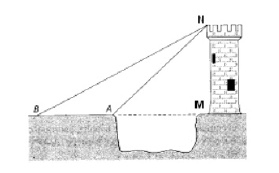
On déduit de la règle des sinus dans le triangle $BAH$ que
$\dfrac{|AH|}{\sin{30^\circ}}=\dfrac{10}{\sin{15^\circ}}\hspace{5mm}\mbox{et donc}\hspace{5mm}|AH|=10\cdot\dfrac{\sin{30^\circ}}{\sin{15^\circ}}.$
Dans le triangle rectangle $AMH$, on a
$ \dfrac{|MH|}{|AH|}=\sin{45^\circ}\hspace{5mm}\mbox{et donc}\hspace{5mm}|MH|=|AH|\cdot\sin{45^\circ}=10\cdot\dfrac{\sin{30^\circ}}{\sin{15^\circ}}\cdot\sin{45^\circ}. $
Puisque $\sin{15^\circ}=\sin{(45^\circ-30^\circ)}=\dfrac{\sqrt{2}}{4}(\sqrt{3}-1)$, on déduit que
$ \begin{array}{rcl} |MH|&=&10\cdot\dfrac{\sin{30^\circ}}{\sin{15^\circ}}\cdot\sin{45^\circ}\\[2mm] &=&10\cdot\dfrac{1}{2}\cdot\dfrac{4}{\sqrt{2}(\sqrt{3}-1)}\cdot\dfrac{\sqrt{2}}{2}\\[2mm] &=&\dfrac{10}{\sqrt{3}-1}=\dfrac{10(\sqrt{3}+1)}{2}=5(\sqrt{3}+1)\mbox{ m}. \end{array} $
Le triangle $AMH$ étant isocèle, on a aussi $|AM|=5(\sqrt{3}+1)\mbox{ m}$.
La hauteur de la tour et la largeur du fossé mesurent donc $5(\sqrt{3}+1)\mbox{ m}$.
Déterminez le centre et le rayon de la sphère $x^2+y^2+z^2+2x-6z=54$.
On a
$ \begin{array}{c} x^2+y^2+z^2+2x-6z=54\\ x^2+2x+1+y^2+z^2-6z+9=54+1+9\\ (x+1)^2+y^2+(z-3)^2=64 \end{array} $
Il s'agit donc d'une sphère de centre $(-1,0,3)$ et de rayon $8$.
Dans la figure ci-dessous, $ABDO$ est un rectangle tel que $|OD| = |DC| = |CB| = \sqrt{2}$.
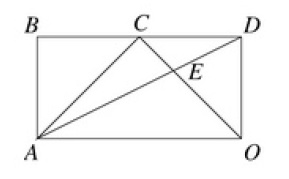
-
Montrez que les triangles $AEO$ et $CED$ sont semblables.
Les angles $\widehat{AEO}$ et $\widehat{CED}$ sont égaux car opposés par le sommet. Les angles $\widehat{EOA}$ et $\widehat{ECD}$ sont égaux car alternes internes. Les angles $\widehat{CDE}$ et $\widehat{EAO}$ sont égaux car alternes internes. On en déduit que les triangles $AEO$ et $CED$ sont semblables.
-
Calculez la distance $|OE|$.
Les triangles $AEO$ et $CED$ étant semblables, on a
$ \dfrac{|EO|}{|CE|}=\dfrac{|AO|}{|CD|}=\dfrac{2\sqrt{2}}{\sqrt{2}}\hspace{5mm}\mbox{et donc}\hspace{5mm}|EO|=2|CE|. $
Par Pythagore dans le triangle $CDO$, on a
$ |CO|^2=|CD|^2+|DO|^2\hspace{5mm}\mbox{et donc}\hspace{5mm}|CO|=2. $
On en déduit que $|OE|=|CO|-|CE|=2-\dfrac{|OE|}{2}$ et donc $|OE|=\dfrac{4}{3}$.
Enoncez le Théorème d'Euler pour les solides.
Dans tout polyèdre convexe, on a $F+S-A=2$ où $F$ est le nombre de faces, $S$ le nombre de sommets et $A$ le nombre d'arêtes du polyèdre.
Les 4 faces latérales d'une pyramide à base carrée sont des triangles équilatéraux.
-
Déterminez la hauteur de cette pyramide sachant que le côté de la base mesure $20\sqrt{2}$ cm.
La hauteur de la pyramide est donnée par $|SO|$ dans le schéma ci-dessous.
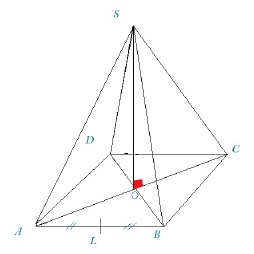
La longueur $|OA|$ est la demi-diagonale du carré de côté $20\sqrt{2}$. On a donc
$ (2|OA|)^2=|AB|^2+|BC|^2=(20\sqrt{2})^2+(20\sqrt{2})^2=800+800=1600 $
et donc $|OA|^2=400$ et $|OA|=20$.
Par Pythagore dans le triangle rectangle $AOS$, on obtient la hauteur $h$ de la pyramide
$ h^2=|SO|^2=|SA|^2-|OA|^2=(20\sqrt{2})^2-400=800-400=400 $
et donc $h=20$ cm.
-
Déterminez le volume de cette pyramide.
Le volume d'une pyramide est donné par la formule $V=\dfrac{bh}{3}$ où $b$ est l'aire de la base et $h$ la hauteur. On obtient donc
$ V=\dfrac{(20\sqrt{2})^2\cdot 20}{3}=\dfrac{16000}{3}\mbox{ cm}^3. $
On considère la droite
$ \Delta=\left\{ \begin{array}{l} \dfrac{x+1}{3}=\dfrac{y-1}{2}\\ \dfrac{y-1}{2}=\dfrac{z}{-1} \end{array} \right. $
-
Déterminez un point et un vecteur directeur de la droite $\Delta$.
Les équations paramétriques de cette droite sont
$ \Delta=\left\{ \begin{array}{l} x=-1+3t\\ y=1+2t\\ z=-t \end{array} \right. $
avec $t\in\mathbb{R}$.
Un point de la droite est par exemple $P_0=(-1,1,0)$ (prendre $t=0$) ou $P_0=(2,3,-1)$ (prendre $t=1$) et un vecteur directeur est $\vec v=(3,2,-1)$.
-
Déterminez la distance du point $P=(1,2,1)$ à la droite $\Delta$.
Pour trouver la distance du point $P$ à la droite $\Delta$ il faut construire un plan $\Pi$ orthogonal à $\Delta$ passant par $P$ et chercher l'intersection $Q$ de ce plan $\Pi$ avec la droite $\Delta$. La distance cherchée est la distance de $P$ à $Q$.
Le plan $\Pi$ orthogonal à $\Delta$ et passant par $P$ a pour vecteur normal le vecteur $\vec v$. Son équation est donc $\Pi\, :\, 3x+2y-z=6$.
L'intersection du plan $\Pi$ avec la droite $\Delta$ s'obtient en résolvant le système
$ \left\{ \begin{array}{l} 3x+2y-z=6\\ x=-1+3t\\ y=1+2t\\ z=-t \end{array} \right. $
c'est-à-dire $3(-1+3t)+2(1+2t)-(-t)=6$. On trouve $t=\frac{1}{2}$ et donc $Q=(\frac{1}{2},2,-\frac{1}{2})$.
La distance du point $P$ à la droite $\Delta$ est donnée par
$ \Vert\overrightarrow{PQ}\Vert=\sqrt{\left(1-\frac{1}{2}\right)^2+(2-2)^2+\left(1+\frac{1}{2}\right)^2}=\sqrt{\frac{10}{4}}=\frac{\sqrt{10}}{2}. $
Les propositions suivantes sont-elles vraies ou fausses ? Répondez par V ou F dans la case à la fin de la phrase, sans justifier. Une mauvaise réponse entraînera l'annulation d'une bonne réponse. Vous pouvez vous abstenir sans être pénalisé.
-
Pour tout $a\in\mathbb{R}$, on a $\cos(2a)=2\cos^2(a)-1$.
Vrai.
-
Les droites $y=3x-2$ et $3y=x+5$ sont perpendiculaires.
Faux.
La pente de la droite $y=3x-2$ vaut $3$ et celle de la droite $3y=x+5$ vaut $\frac{1}{3}$. Vu que $3\cdot\frac{1}{3}\neq -1$, ces droites ne sont pas perpendiculaires.
-
Le vecteur $(3,1)$ est perpendiculaire à la droite $y=3x-4$.
Faux.
La pente de la droite $y=3x-4$ vaut $3$. Le vecteur $(1,3)$ est donc un vecteur directeur de la droite et comme $(1,3)\odot (3,1)=3+3=6\neq 0$, le vecteur $(3,1)$ n'est pas perpendiculaire à la droite.
-
En topologie, une fourchette est une surface de genre 2.
Faux.
Une fourchette peut être déformée en un disque. C'est donc une surface de genre $0$.
-
On peut inscrire tout triangle rectangle dans un demi-cercle dont le rayon est l'hypoténuse du triangle.
Faux.
On peut inscrire tout triangle rectangle dans un demi-cercle dont le diamètre est l'hypoténuse du triangle.
Ecrivez la réponse correcte dans la case à la fin de la phrase sans justifier.
-
Déterminez l'axe de symétrie de la parabole $y=2x^2-8x+5$.
L'axe de symétrie est donné par l'équation $x=-\frac{b}{2a}$. Ici on obtient $x=2$
-
Donnez les composantes du vecteur $\vec{u}\times\vec{v}$ si $\vec{u}=(1,3,2)$ et $\vec{v}=(4,-1,-2)$.
On calcule $\vec{u}\times\vec{v}=(3\cdot(-2)-2\cdot(-1),2\cdot 4-1\cdot(-2),1\cdot(-1)-3\cdot 4)=(-4,10,-13)$.
-
Donnez l'équation du second degré dont le nombre d'or est solution.
Le nombre d'or est solution de l'équation $x^2-x-1=0$.
-
Donnez le milieu du segment joignant $A$ et $B$ si $A=(-1,5,2)$ et $B=(3,3,4)$.
Le milieu du segment joignant $A$ et $B$ est donné par la formule $\frac{A+B}{2}=(1,4,3)$.
-
Calculez la distance du point $P=(2,-1,-1)$ au plan $\Pi\, :\, 16x-12y+15z-4=0$.
Un vecteur normal au plan $\Pi$ est le vecteur $\vec n=(16,-12,15)$. La distance de $P$ à $\Pi$ est donnée par
$d(P,\Pi)=\dfrac{|2\cdot 16+(-1)\cdot(-12)+(-1)\cdot 15-4|}{\sqrt{16^2+(-12)^2+15^2}}=\dfrac{25}{\sqrt{625}}=1.$