Examen de Mai 2017
Pour vous tester, essayez de résoudre cet ancien examen.
Enoncez et démontrez le Théorème des médianes.
La somme des carrés des longueurs de deux côtés d'un tiangle est égale à deux fois le carré de la longueur de la médiane relative au troisième côté plus deux fois le carré de la moitié de la longueur du troisième côté : $$b^2+c^2=2m^2+2\left(\dfrac{a}{2}\right)^2.$$
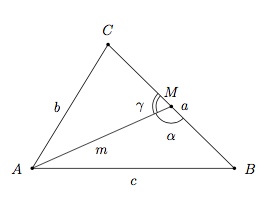
La démonstration se trouve dans le syllabus à la page 53.
On considère le trapèze rectangle $ABCD$ ci-dessous avec $|AB|=5$ cm, $|AD|=4$ cm et $\widehat{DCB}=60^{\circ}$. Déterminez les valeurs exactes du périmètre et de l'aire de ce trapèze.
Soit $E$ la projection orthogonale de $B$ sur $DC$.
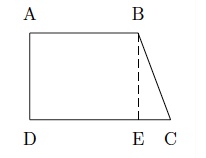
On a $$\mbox{tg }60^{\circ}=\dfrac{|BE|}{|EC|}\mbox{ d'où }|EC|=\dfrac{|BE|}{\mbox{tg }60^{\circ}}=\dfrac{4}{\sqrt{3}}=\dfrac{4\sqrt{3}}{3}.$$
De plus, par Pythagore, on obtient $$|BC|^2=|BE|^2+|EC|^2=16+\dfrac{16}{3}=\dfrac{64}{3}\mbox{ et donc }|BC|=\dfrac{8\sqrt{3}}{3}.$$
Le périmètre du trapèze vaut donc $$P=5+4+5+\dfrac{4\sqrt{3}}{3}+\dfrac{8\sqrt{3}}{3}=14+4\sqrt{3}\mbox{ cm}$$ et son aire vaut $$A=\left(5+5+\dfrac{4\sqrt{3}}{3}\right)\cdot 4\cdot\dfrac{1}{2}=20+\dfrac{8\sqrt{3}}{3}\mbox{ cm}^2.$$
On considère les deux plans $\Pi_1\, :\, x-2y+3z+1=0$ et $\Pi_2\, :\, kx+y-5z-3=0$.
-
Déterminez $k\in\mathbb{R}$ pour que $\Pi_1$ et $\Pi_2$ soient orthogonaux.
Soit $\vec{n}_1=(1,-2,3)$ et $\vec{n}_2=(k,1,-5)$ des vecteurs normaux aux plans $\Pi_1$ et $\Pi_2$ respectivement.
Les plans $\Pi_1$ et $\Pi_2$ sont orthogonaux si et seulement si les vecteurs $\vec{n}_1$ et $\vec{n}_2$ sont orthogonaux, c'est-à-dire si $\vec{n}_1\odot\vec{n}_2=0$. On en déduit $k=17$.
-
Pour cette valeur de $k$, déterminez l'intersection des plans $\Pi_1$ et $\Pi_2$. De quelle forme géométrique s'agit-il ?
L'intersection de ces deux plans est une droite d'équation $$\left\{\begin{array}{l}x-2y+3z+1=0\\17x+y-5z-3=0\end{array}\right.$$
Soit $P=(1,2,5)$ et $Q=(3,-4,1)$.
-
Donnez l'équation cartésienne de la droite $\Delta$ joignant $P$ à $Q$.
Un vecteur directeur de la droite est le vecteur $\overrightarrow{PQ}=(2,-6,-4)$. La droite $\Delta$ a donc pour équation $$\left\{\begin{array}{l}\dfrac{x-1}{2}=\dfrac{y-2}{-6}\\\dfrac{y-2}{-6}=\dfrac{z-5}{-4}\end{array}\right.$$ ou encore $$\left\{\begin{array}{l}3x+y=5\\2y-3z=-11\end{array}\right.$$
-
Donnez l'équation du plan médiateur du segment $PQ$.
Le vecteur $\overrightarrow{PQ}=(2,-6,-4)$ est un vecteur normal au plan médiateur. De plus, celui-ci passe par le point $M=\frac{1}{2}(4,-2,6)=(2,-1,3)$. Le plan médiateur a donc pour équation $$2x-6y-4z=4+6-12$$ ou encore $$x-3y-2z=-1.$$
-
Le point $R=(-1,8,-12)$ appartient-il à la droite $\Delta$ ? et au plan médiateur ? Justifiez.
Le point $R$ n'appartient pas à la droite $\Delta$ car $2\cdot 8-3\cdot (-12)=16+36\neq -11$.
Le point $R$ appartient au plan médiateur car $-1-3\cdot 8-2\cdot (-12)=-1-24+24=-1$.
Résolvez l'équation $4\sin^2{x}=-\sqrt{3}\, \mbox{tg }x$, $x\in [0,\pi]$.
On a $$4\sin^2{x}=-\sqrt{3}\, \dfrac{\sin{x}}{\cos{x}}.$$
$\bullet\, $ soit $\sin{x}=0$ d'où $x=k\pi$ avec $k\in\mathbb{Z}$;
$\bullet\, $ soit $4\sin{x}=\dfrac{-\sqrt{3}}{\cos{x}}$, d'où $4\sin{x}\cos{x}=-\sqrt{3}$ et $2\sin{2x}=-\sqrt{3}$. On en déduit $2x=\frac{4\pi}{3}+2k\pi$ ou $2x=\frac{5\pi}{3}+2k\pi$ et donc $x=\frac{2\pi}{3}+k\pi$ ou $x=\frac{5\pi}{6}+k\pi$.
Les solutions dans l'intervalle $[0,\pi]$ sont données par $$S=\left\{0,\, \frac{2\pi}{3},\, \frac{5\pi}{6},\, \pi\right\}.$$
Le nombre d'or.
-
Donnez la valeur du nombre d'or.
Le nombre d'or est $\phi=\dfrac{1+\sqrt{5}}{2}$.
-
Donnez une équation du second degré dont le nombre d'or est solution. Justifiez.
Le nombre d'or est solution de l'équation $x^2-x-1=0$. En effet, on a $$\begin{array}{rcl}\left(\dfrac{1+\sqrt{5}}{2}\right)^2-\dfrac{1+\sqrt{5}}{2}-1&=&\dfrac{1+5+2\sqrt{5}}{4}-\dfrac{1+\sqrt{5}}{2}-1=0\end{array}$$
-
Construisez précisément à la règle et au compas un segment dont la longueur est le nombre d'or. Expliquez votre construction.
Soit $ABCD$ un carré de côté $1$ et $E$ le milieu de $CD$. On trace le cercle de centre $E$ et de rayon $EA$.
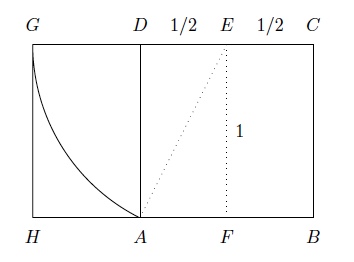
Le segment $GC$ est de longueur $\phi$. En effet, $r=|EA|=\sqrt{1+\frac{1}{4}}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2}$ et donc $$|GC|=|GE|+|EC|=|EA|+\dfrac{1}{2}=\dfrac{\sqrt{5}}{2}+\dfrac{1}{2}=\dfrac{\sqrt{5}+1}{2}=\phi.$$
Soit $P=(-4,0)$ et $Q=(4,0)$. Démontrez que tout triangle $PQR$ inscrit dans le demi-cercle de base $\overrightarrow{PQ}$ est rectangle.
Soit $R=(x,y)$ un point du demi-cercle. On a donc $x^2+y^2=16$. On calcule $\overrightarrow{PR}=(x+4,y)$, $\overrightarrow{QR}=(x-4,y)$ et $$\overrightarrow{PR}\odot\overrightarrow{QR}=(x+4)(x-4)+y^2=x^2-16+y^2=0.$$ Cela implique que $\overrightarrow{PR}\perp\overrightarrow{QR}$ et donc que le triangle $PQR$ a un angle droit en $R$.
Un rayon lumineux est issu du point $M=(2,3)$ sous un angle $\alpha$ avec l'axe $OX$. On sait que $\mbox{tg }\alpha=4$. Ayant atteint l'axe horizontal, le rayon est réfléchi (avec un angle de réflexion égal à l'angle d'incidence). Donnez les équations des droites qui portent les rayons incident et réfléchis.
Soit $\Delta_1$ la droite qui porte le rayon incident et $\Delta_2$ celle qui porte le rayon réfléchis.
Vu que $\mbox{tg }\alpha =4$, on en déduit que la pente de $\Delta_1$ vaut $4$. De plus $\Delta_1$ contient le point $(2,3)$ et donc $\Delta_1$ a pour équation $y=4x-5$.
L'intersection de $\Delta_1$ avec l'axe $OX$ donne le point $(\frac{5}{4},0)$. Ce point appartient à la droite $\Delta_2$. Puisque l'angle de réflexion est égal à l'angle d'incidence, la pente de la droite $\Delta_2$ vaut $-4$. On en déduit que la droite $\Delta_2$ a pour équation $y=-4x+5$.
Les propositions suivantes sont-elles vraies ou fausses ? Répondez par V ou F dans la case à la fin de la phrase, sans justifier. Une mauvaise réponse entraînera l'annulation d'une bonne réponse. Vous pouvez vous abstenir sans être pénalisé.
-
Dans un triangle, la longueur du segment qui joint le milieu de deux côtés vaut la moitié de la longueur du troisième côté.
Vrai.
-
Dans tout polyèdre convexe, on a $S+A-F=2$ où $S$, $A$ et $F$ représentent le nombre de sommets, arêtes et faces.
Faux. On a on a $S+F-A=2$.
-
Le centre du cercle circonscrit à un triangle est le point d'intersection de ses trois médiatrices.
Vrai.
-
Pour tout $x\in\mathbb{R}$, on a $\cos^2{x}-\sin^2{x}=1$.
Faux. On a $\cos^2{x}+\sin^2{x}=1$.
-
Si on permute deux axes d'un repère orthonormé de $\mathbb{R}^3$ alors son orientation change.
Vrai.
Ecrivez la réponse correcte dans la case à la fin de la phrase sans justifier.
-
Si $\theta$ est un angle du second quadrant dont le sinus vaut $\frac{3}{4}$, quelle est la valeur de $\mbox{tg }\theta$ ?
On peut représenter la situation par un triangle rectangle dont le côté opposé à $\theta$ vaut $3$ et l'hypoténuse vaut $4$. Le côté adjacent à $\theta$ vaut donc $x=\sqrt{4^2-3^2}=\sqrt{7}$. On en déduit $\mbox{tg }\theta=\dfrac{3}{\sqrt{7}}=\dfrac{3\sqrt{7}}{7}$. Comme $\theta$ appartient au second quadrant, sa tangente est négative et donc $\mbox{tg }\theta=-\dfrac{3\sqrt{7}}{7}$.
-
Soit $\vec{a}=(2,-3,1)$ et $\vec{b}=(-5,2,3)$. Calculez $\vec{a}\times\vec{b}$.
Soit $\vec{u}=(u_x,u_y,u_z)$ et $\vec{v}=(v_x,v_y,v_z)$. Les composantes du vecteur $\vec{u}\times\vec{v}$ sont données par $$\vec{u}\times\vec{v}=(u_yv_z-u_zv_y,u_zv_x-u_xv_z, u_xv_y-u_yv_x).$$
On calcule $\vec a\times\vec b=(-3\cdot 3-2\cdot 1,1\cdot(-5)-2\cdot 3,2\cdot 2-(-3)\cdot -5)=(-11,-11,-11)$.
-
Donnez l'équation de la sphère centrée au point $C=(-3,2,5)$ et passant par l'origine $(0,0,0)$.
Pour trouver le rayon de cette sphère, on calcule la distance entre l'origine et le point $C$ . Le rayon de cette sphère est donc donné par $$ r=\sqrt{(-3-0)^2+(2-0)^2+(5-0)^2}=\sqrt{9+4+25}=\sqrt{38}. $$ L'équation de la sphère est $$ (x+3)^2+(y-2)^2+(z-5)^2=38. $$
-
Soit $A=(1,2,3)$ et $B=(3,2,2)$. Donnez la longueur du segment joignant $A$ et $B$.
La longueur du segment joignant $A$ et $B$ est donnée par $$\sqrt{(3-1)^2+(2-2)^2+(2-3)^2}=\sqrt{4+1}=\sqrt{5}.$$
-
Calculez le volume du parallélipipède construit sur les vecteurs $\vec{a}=(2,-3,1)$, $\vec{b}=(-5,2,3)$ et $\vec{c}=(1,2,3)$ (où $\vec{a}$ et $\vec{b}$ forment la base du parallélipipède).
Le volume du parallélipipède est donné par $|(\vec a\times\vec b)\odot\vec c|$.
On calcule $\vec a\times\vec b=(-3\cdot 3-2\cdot 1,1\cdot(-5)-2\cdot 3,2\cdot 2-(-3)\cdot -5)=(-11,-11,-11)$ et donc $$V=|(-11,-11,-11)\odot(1,2,3)|=|-11-22-33|=|-66|=66.$$