Examen de Mai 2018
Pour vous tester, essayez de résoudre cet ancien examen.
Soit $(x,y)$, les coordonnées cartésiennes d'un point $P$ du plan. Expliquez comment trouver les coordonnées polaires $(r,\theta)$ de ce point en fonction de $x$ et $y$.
On a $$ \left\{\begin{array}{l} r=\sqrt{x^2+y^2}\\ \tan{\theta}=\dfrac{y}{x}\mbox{ si }x\neq 0\\ \theta=\dfrac{\pi}{2}\mbox{ si }x=0,\, y>0\\ \theta=\dfrac{3\pi}{2}\mbox{ si }x=0,\, y<0 \end{array}\right. $$
On considère le solide d'équation $x^2+y^2+z^2-6x+2y=6$.
-
Vers quel point faut-il translater l'origine du repère pour que cette équation ne contienne plus de termes du premier degré ?
On effectue une translation vers le point $(a,b,c)$. Il faut trouver les valeurs de $a$, $b$ et $c$ pour supprimer les termes du premier degré.
$$ \left\{ \begin{array}{l} x=a+x'\\ y=b+y'\\ z=c+z' \end{array} \right. $$
On remplace dans l'équation $$ (a+x')^2+(b+y')^2+(c+z')^2-6(a+x')+2(b+y')=6. $$
Il faut que $$ \left\{ \begin{array}{l} 2a-6=0\\ 2b+2=0\\ 2c=0 \end{array} \right. $$
donc que $a=3$, $b=-1$ et $c=0$. Il faut donc translater vers le point $(3,-1,0)$ pour supprimer les termes du premier degré.
-
Que devient cette équation après la translation ?
L'équation devient $$(3+x')^2+(-1+y')^2+(z')^2-6(3+x')+2(-1+y')=6$$
$$(x')^2+(y')^2+(z')^2=16$$
-
De quel solide s'agit-il ? Justifiez en donnant ses caractéristiques.
Il s'agit d'une sphère de centre $(0,0,0)$ et de rayon $4$ dans le nouveau repère, c'est-à-dire d'une sphère centrée en $(3,-1,0)$ et de rayon $4$ dans le repère de départ.
Enoncez et démontrez la formule qui permet de trouver la distance du point $P=(x_0,y_0,z_0)$ au plan $\Pi$ d'équation $ax+by+cz+d=0$.
La distance du point $P=(x_0,y_0,z_0)$ au plan $\Pi$ d'équation $ax+by+cz+d=0$ est donnée par la formule
$$d(P,\Pi)=\dfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}.$$
La démonstration se trouve dans le syllabus à la page 138.
On considère le plan $\Pi\, :\, 3x-4z+25=0$.
-
Déterminez la distance du point $P=(-1,1,3)$ au plan $\Pi$.
La distance du point $P=(-1,1,3)$ au plan $\Pi\, :\, 3x-4z+25=0$ est donnée par la formule
$$d(P,\Pi)=\dfrac{|3\cdot (-1)+0\cdot 1+(-4)\cdot 3+25|}{\sqrt{3^2+0^2+(-4)^2}}=\dfrac{|-3-12+25|}{\sqrt{9+16}}=2.$$
-
Déterminez l'équation cartésienne de l'autre plan parallèle au plan $\Pi$ et dont la distance au point $P$ est la même.
Ce plan $\Pi'$ a pour équation $3x-4z+d=0$. Pour que la distance de $P$ à $\pi'$ soit égale à 2, il faut que
$$\dfrac{|3\cdot (-1)+0\cdot 1+(-4)\cdot 3+d|}{\sqrt{3^2+0^2+(-4)^2}}=2$$
$$\dfrac{|-3-12+d|}{5}=2$$
$$|d-15|=10$$
et donc $d=25$ ou $d=5$. Le plan cherché a donc pour équation $3x-4z+5=0$.
Résolvez l'équation $3(1-\cos{x})=\sin^2{x}$.
On a
$$3-3\cos{x}=1-\cos^2{x}$$
$$\cos^2{x}-3\cos{x}+2=0$$
En posant $t=\cos{x}$, on trouve $t=2$ ou $t=1$.
$\bullet\, $ soit $t=\cos{x}=2$ ce qui est impossible;
$\bullet\, $ soit $t=\cos{x}=1$, d'où $x=2k\pi$.
Les solutions sont données par
$$S=\left\{2k\pi;\, k\in\mathbb{Z}\right\}.$$
Calculez la hauteur d'une tour dressée au bord d'une falaise sachant qu'à $100$ m, on voit la falaise sous un angle de $30^{\circ}$ et la tour sous un angle de $15^{\circ}$ supplémentaires.
On peut représenter la situation par le schéma ci-dessous
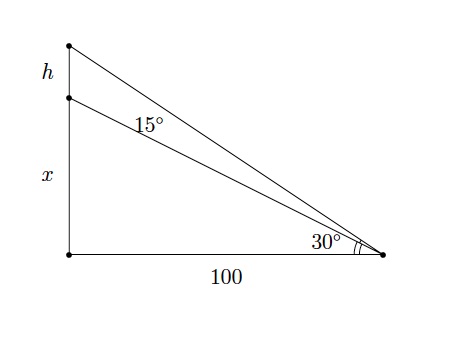
On a $x+h=100$ car le triangle est isocèle.
De plus, $\tan{30^\circ}=\dfrac{x}{100}=\dfrac{100-h}{100}$ et donc $h=100-100\cdot \dfrac{\sqrt{3}}{3}$ m.
On considère le parallélipipède rectangle ci-dessous.
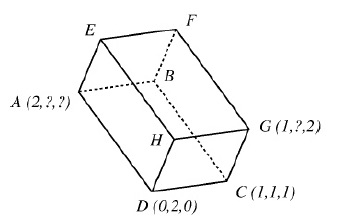
-
Déterminez les coordonnées des points $G$, $A$, et $F$.
Soit $G=(1,y,2)$. On a $\overrightarrow{CG}\perp\overrightarrow{CD}$ et donc
$$\overrightarrow{CG}\odot\overrightarrow{CD}=(0,y-1,1)\odot(-1,1,-1)=0.$$
On en déduit $y-2=0$ d'où $y=2$ et $G=(1,2,2)$.
Soit $A=(2,y,z)$. On a $\overrightarrow{DA}\perp$ plan $DCG$ donc $\overrightarrow{DA}=k(\overrightarrow{CD}\times\overrightarrow{CG})=k(2,1,-1)$. On obtient $\overrightarrow{DA}=(2,y-2,z)=k(2,1,-1)$ et donc $k=1$ et $A=(2,3,-1)$.
Soit $F=(x,y,z)$. On a $\overrightarrow{GF}=\overrightarrow{DA}$ d'où
$$\overrightarrow{GF}=(x-1,y-2,z-2)=(2,1,-1).$$
On en déduit $F=(3,3,1)$.
-
Donnez l'équation cartésienne des plans $DCG$ et $ABF$. Précisez leurs vecteurs normaux.
On a $\vec{n}=\overrightarrow{CD}\times\overrightarrow{CG}=(2,1,-1)$ et donc le plan $DCG$ a pour équation $2x+y-z=2$ et le plan $ABF$ a pour équation $2x+y-z=8$.
-
Donnez l'équation cartésienne de la droite $EF$. Précisez son vecteur directeur.
On a $\vec{v}=\overrightarrow{CD}=(-1,1,-1)$ et donc la droite $EF$ a pour équation $$ \left\{\begin{array}{l} \dfrac{x-3}{-1}=\dfrac{y-3}{1}\\ \dfrac{y-3}{1}=\dfrac{z-1}{-1} \end{array}\right. $$
c'est-à-dire $$ \left\{\begin{array}{l} x+y=6\\ y+z=4 \end{array}\right. $$
-
Déterminez la surface du rectangle $DCGH$.
La surface est donnée par
$$S=\Vert \overrightarrow{CD}\times\overrightarrow{CG}\Vert=\Vert(2,1,-1)\Vert=\sqrt{6}.$$
-
Déterminez le volume de ce parallélipipède rectangle.
Le volume est donné par
$$V=\vert(\overrightarrow{CD}\times\overrightarrow{CG})\odot \overrightarrow{DA}\vert=\vert(2,1,-1)\odot (2,1,-1)\vert=6.$$
Les propositions suivantes sont-elles vraies ou fausses ? Répondez par V ou F dans la case à la fin de la phrase, sans justifier. Une mauvaise réponse entraînera l'annulation d'une bonne réponse. Vous pouvez vous abstenir sans être pénalisé.
-
Dans un triangle, le centre de gravité, l'orthocentre et le centre du cercle circonscrit sont toujours alignés.
Vrai
-
Si $P=(2,-2,8)$ et $Q=(-1,2,3)$ alors le milieu du segment qui relie $P$ à $Q$ est $M=(\frac{3}{2},-2,\frac{5}{2})$.
Faux. Le milieu du segment qui relie $P$ à $Q$ est $M=(\frac{1}{2},0,\frac{11}{2})$.
-
Les vecteurs $\overrightarrow{a}=(2,3,1)$ et $\overrightarrow{b}=(-5,3,1)$ sont orthogonaux.
Vrai
-
Si on triple le rayon d'un cône et on divise par quatre sa hauteur alors son volume est multiplié par $\frac{3}{4}$.
Faux. Son volume est multiplié par $\frac{9}{4}$.
-
Le point $P=(2,-2\sqrt{3})$ se trouve à distance $16$ de l'origine.
Faux. Le point $P$ se trouve à distance $\sqrt{16}$ de l'origine.
Ecrivez la réponse correcte dans la case à la fin de la phrase sans justifier.
-
Donnez l'équation de l'axe de symétrie de la parabole $y=3x^2-6x+5$.
L'axe de symétrie de cette parabole a pour équation $x=1$.
-
Les diagonales d'un losange mesurent $8$ cm et $10$ cm. Calculez la longueur des côtés du losange.
Le côté du losange mesure $\sqrt{(\frac{8}{2})^2+(\frac{10}{2})^2}=\sqrt{41}$ cm.
-
Donnez l'équation du plan médiateur au segment reliant $A=(5,-3,0)$ et $B=(1,5,-2)$.
Le plan médiateur du segment $AB$ est perpendiculaire à ce segment et passe par son milieu. Le milieu est donné par $M=(3,1,-1)$ et un vecteur normal au plan est $\overrightarrow{AB}=(-4,8,-2)$. Ce plan a donc pour équation $-4x+8y-2z=-12+8+2$, c'est-à-dire $2x-4y+z=1$.
-
Déterminez $k\in\mathbb{R}$ pour que les plans $\pi_1\, :\, x-2y+3z+1=0$ et $\pi_2\, :\, kx+y-5z-3=0$ soient perpendiculaires.
Les plans sont perpendiculaires si leurs vecteurs normaux sont perpendiculaires donc si $$(1,-2,3)\odot(k,1,-5)=0$$ $$k-2-15=0$$ et donc $k=17$.
-
Dans une sphère dont le rayon vaut $7$ cm, on inscrit un cône circulaire droit dont la hauteur vaut $10$ cm. Que vaut le rayon de la base du cône ?
Le rayon de la base vaut $\sqrt{7^2-3^2}=\sqrt{40}$ cm.