Questions de théorie

La somme des mesures des angles dans un triangle vaut toujours $180^\circ = \pi$ radians, c'est-à-dire $\alpha+ \beta+\gamma=180^\circ$.

Dans tout triangle, la droite passant par le milieu d'un côté et parallèle à un autre côté coupe le troisième côté en son milieu.

Réciproquement, dans tout triangle, le segment joignant les milieux de deux des côtés est parallèle au troisième côté et sa longueur vaut la moitié de celle de ce troisième côté.

La médiatrice d'un segment est la droite perpendiculaire au milieu de ce segment.

Tous les points de cette droite sont à même distance des extrémités du segment. Réciproquement, tout point équidistant des extrémités d'un segment appartient à la médiatrice de ce segment.

Une médiatrice d'un triangle est une droite perpendiculaire au milieu d'un de ses côtés.

Un triangle a donc 3 médiatrices.  Les trois médiatrices d'un triangle se coupent en un même point.

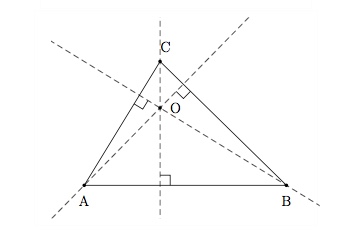
On considère le triangle quelconque $ABC$ et soit $m_1$ médiatrice du côté $AB$, $m_2$ médiatrice du côté $AC$ et $m_3$ médiatrice du côté $BC$. Soit $X$ le point d'intersection de $m_1$ et $m_2$.

Voyons que $m_1$, $m_2$ et $m_3$ se coupent au point $X$.

Puisque $X\in m_1$, on a que les segments $XA$ et $XB$ sont de même longueur. De même, puisque $X\in m_2$, on a que les segments $XA$ et $XC$ sont de même longueur. On endéduit que les segments $XB$ et $XC$ sont de même longueur et donc que $X$ est un point de la médiatrice $m_3$.

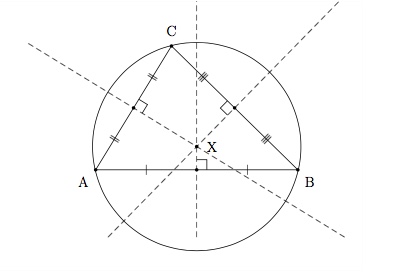
Le point d'intersection des trois médiatrices d'un triangle se trouve à égale distance des trois sommets du triangle. Ce point est donc le centre du cercle circonscrit au triangle. Par trois points non alignés, on peut donc faire passer un et un seul cercle.

La bissectrice d'un angle est la droite qui coupe cet angle en deux angles de même amplitude.

Tous les points de cette droite sont à même distance des côtés de l'angle. Réciproquement, tout point équidistant des côtés d'un angle appartient à la bissectrice de cet angle.

Une bissectrice d'un triangle est une droite qui coupe un de ses angles en deux angles de même amplitude.

Un triangle a donc 3 bissectrices.  Les trois bissectrices d'un triangle se coupent en un même point.

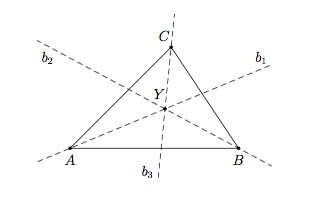
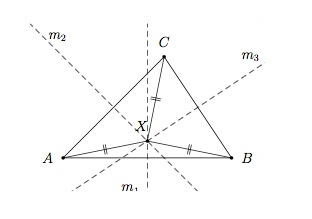
On considère le triangle quelconque $ABC$ et soit $b_1$ bissectrice de l'angle $BAC$, $b_2$ bissectrice de l'angle $ABC$ et $b_3$ bissectrice de l'angle $BCA$. Soit $Y$ le point d'intersection de $b_1$ et $b_2$.

Voyons que $b_1$, $b_2$ et $b_3$ se coupent au point $Y$.

Tous les points de la droite $b_1$ sont à même distance des côtés $AB$ et $AC$ et tous les points de la droite $b_2$ sont à même distance des côtés $BA$ et $BC$. Puisque $Y\in b_1$ et $Y\in b_2$, on a que $Y$ est à même distance des côtés $AC$ et $BC$. On en déduit que $Y$ est un point de la bissectrice $b_3$.

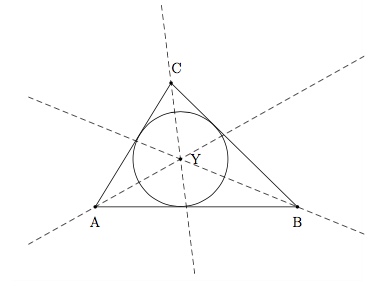
Le point d'intersection des trois bissectrices d'un triangle se trouve à égale distance des trois côtés du triangle. Ce point est donc le centre du cercle inscrit au triangle. Ce cercle est tangent à chaque côté du triangle.

Une médiane d'un triangle est une droite qui relie un des sommets au milieu du côté opposé.

Un triangle a donc 3 médianes.  Les trois médianes d'un triangle se coupent en un même point.

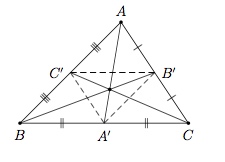
On considère le triangle quelconque $ABC$ et soit $A'$ le milieu du segment $BC$, $B'$ le milieu du segment $AC$ et $C'$ le milieu du segment $AB$.

On déduit de la proposition C06 que $C'B'\parallel BC$ et que la longueur du segment $BC$ est le double de celle du segment $B'C'$.

De même, la longueur du segment $AB$ est le double de celle du segment $A'B'$ et la longueur du segment $AC$ est le double de celle du segment $A'C'$.

Les triangles $ABC$ et $A'B'C'$ sont donc semblables et le triangle $A'B'C'$ est l'image du triangle $ABC$ par une homothétie. Les droites $AA'$, $BB'$ et $CC'$ sont donc concourantes.

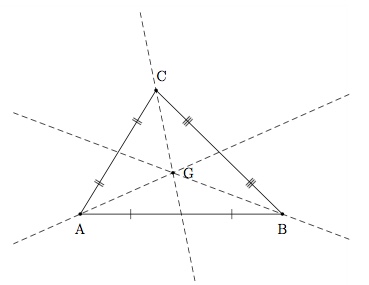
Le point d'intersection des trois médianes est le centre de gravité du triangle. Il est situé sur chaque médiane aux $2/3$ de chacune d'elle à partir du sommet.

Une hauteur d'un triangle est une droite passant par un sommet et perpendiculaire au côté opposé (ou à son prolongement).

Un triangle a donc 3 hauteurs.  Les trois hauteurs d'un triangle se coupent en un même point.

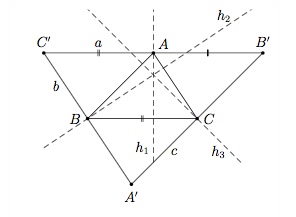
On considère le triangle quelconque $ABC$ et soit $h_1$ hauteur passant par $A$, $h_2$ hauteur passant par $B$ et $h_3$ hauteur passant par $C$.

Traçons la droite $a$ passant par $A$ et parallèle au côté $BC$, la droite $b$ passant par $B$ et parallèle au côté $AC$ et la droite $c$ passant par $C$ et parallèle au côté $AB$. Soit $A'$ le point d'intersection de $b$ et $c$, $B'$ le point d'intersection de $a$ et $c$ et $C'$ le point d'intersection de $a$ et $b$.

Puisque $b\parallel AC$ et $a\parallel BC$, on en déduit que $ACBC'$ est un parallélogramme et donc les segments $C'A$ et $BC$ ont même longueur. De même, puisque $c\parallel AB$ et $a\parallel BC$, on en déduit que $AB'CB$ est un parallélogramme et donc les segments $AB'$ et $BC$ ont même longueur. Cela implique que les segments $C'A$ et $AB'$ ont même longueur et donc $A$ est au milieu du segment $B'C'$.

De plus, $h_1\perp BC$ et $BC\parallel B'C'$ donc $h_1\perp B'C'$. On en déduit que $h_1$ est la médiatrice du segment $B'C'$.

De la même façon, on montre que $h_2$ est la médiatrice du segment $A'C'$ et $h_3$ est la médiatrice du segment $A'B'$.

Puisque les trois médiatrices du triangle $A'B'C'$ se coupent en un même point, on en déduit que $h_1$, $h_2$ et $h_3$ se coupent en un même point.

Le point d'intersection des trois hauteurs est l'orthocentre du triangle.

Dans tout triangle, le centre de gravité, l'orthocentre et le centre du cercle circonscrit sont alignés. La droite qui les contient s'appelle droite d'Euler.