Exercices pour s’entraîner
Entraînez-vous à résoudre les exercices suivants.
-
Déterminez le nombre de sommets, arètes et faces du solide ci-dessous et vérifiez la relation d'Euler.

Ce solide a 17 sommets, 32 arètes et 17 faces.
On a bien $S+F-A=17+17-32=2$.
-
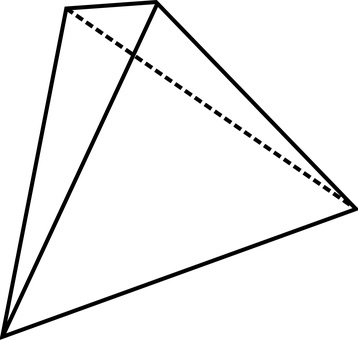
Déterminez le nombre de faces d'un solide qui a 4 sommets et 6 arètes. Représentez un tel solide.
On déduit de la relation d'Euler que $F=2-S+A=2-4+6=4$. Ce solide a donc 4 faces. Une représentation est par exemple
-
Donnez le nom du solide ci-dessous. Déterminez le nombre de sommets, arètes et faces et vérifiez la relation d'Euler.
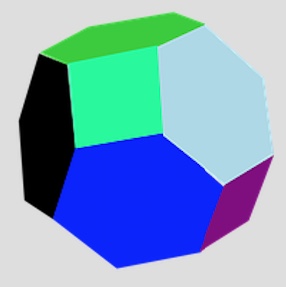
Il s'agit d'un octaèdre tronqué. Il possède 6 faces carrées et 8 faces hexagonales.
Ce solide a 24 sommets, 36 arètes et 14 faces.
On a bien $S+F-A=24+14-36=2$.
-
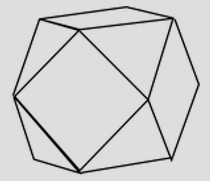
Déterminez le nombre d'arètes d'un solide qui a 12 sommets, 8 faces triangulaires et 6 faces carrées. Représentez un tel solide.
On déduit de la relation d'Euler que $A=S+F-2=12+14-2=24$. Ce solide a donc 24 arètes.
Il s'agit du cuboctaèdre. Une représentation est par exemple
-
Si on coupe le solide ci-dessous par un plan parallèle à ses bases, quelle forme géométrique obtient-on ?
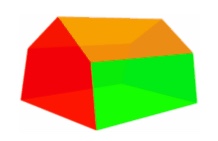
La forme obtenue est un polygone.
On obtient un pentagone non régulier.