Questions de théorie

Le plan $\mathbb{R}^2$ est l'ensemble $\left\{(x,y);\, x\in\mathbb{R}, y\in\mathbb{R}\right\}$.

Un repère cartésien orthonormé du plan est constitué de deux droites perpendiculaires, chacune munie de la même unité de longueur, qui se coupent en leur point origine.

Dans un repère cartésien orthonormé du plan, la droite horizontale est appeéee l'axe des $x$ ou axe $OX$ ou axe des abscisses et la droite verticale est l'axe des $y$ ou axe $OY$ ou axe des ordonnées.

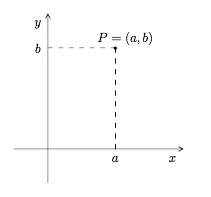
D'un point $P$ quelconque du plan, on mène des parallèles aux axes qui coupent ceux-ci en $a$ pour l'axe des $x$ et en $b$ pour l'axe des $y$. Le point $P$ est ainsi associé au couple de nombres réels $(a,b)$.

Inversément, à tout couple de nombres réels $(a,b)$, en menant des parallèles aux axes passant par $a$ porté sur l'axe des $x$ et par $b$ porté sur l'axe des $y$, on fait correspondre l'unique point d'intersection de ces deux droites.

Le couple $(a,b)$ est appelé coordonnées cartésiennes du point $P$. Le nombre $a$ est l'abscisse de $P$ et le nombre $b$ est son ordonnée.

La distance entre deux points $P=(x_p,y_p)$ et $Q=(x_q,y_q)$ de $\mathbb{R}^2$ est donnée par la formule

$$d(P,Q)= \sqrt{(x_q -x_p)^2 + (y_q-y_p)^2}.$$

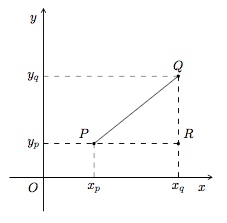
Cette formule est une application immédiate du Théorème de Pythagore au triangle rectangle $PQR$ ci-dessus :

$$(d(P,Q))^2=(x_q-x_p)^2+(y_q-y_p)^2.$$

La distance entre deux points $A=(a,b)$ et $B=(c,d)$ est donnée par la formule

$$d(A,B)= \sqrt{(c-a)^2 + (d-b)^2}.$$

La distance entre les points $O=(0,0)$ et $A=(a,b)$ est donnée par la formule

$$d(O,A)= \sqrt{(a-0)^2 + (b-0)^2}=\sqrt{a^2+b^2}.$$

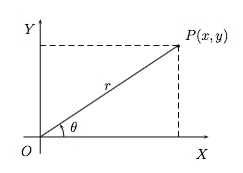
Pour préciser la position d'un point $P$ dans le plan on peut donner les informations suivantes

$\bullet\, $ la distance de $P$ à l'origine, notée $r$ ($r>0$),

$\bullet\, $ l'angle entre l'axe $OX$ et $OP$, noté $\theta $.  Par convention, $\theta\in [0,2\pi[\, $.

Ce sont les coordonnées polaires du point $P$.

Vu que $r$ est la distance de $P$ à l'origine, on a $$r =\sqrt{x^2 + y^2 }.$$

Pour $\theta$, on a

$$ \left\{ \begin{array}{rl} \theta =\frac{\pi}{2}&\mbox{si }x = 0,\, y > 0\\ \theta=\frac{3\pi}{2}&\mbox{si }x = 0,\, y< 0\\ \mbox{tg }\theta=\frac{y}{x}&\mbox{si }x \neq 0 \end{array} \right. $$

La dernière égalité nous permet de trouver $\theta$ selon les signes de $x$ et $y$.

On a $$\left\{ \begin{array}{l} x = r \cos \theta\\ y = r \sin \theta \end{array}\right. $$