Questions de théorie

Le travail $W$ d'une force d'intensité constante $\overrightarrow{F}$ appliquée à un point en mouvement le long d'un vecteur $\overrightarrow{d}$ est $W=\overrightarrow{F}\odot\overrightarrow{d}$.

Supposons que le vecteur $\overrightarrow{F}$ représente une force et que le point où cette force est appliquée se déplace le long d'un vecteur $\overrightarrow{d}$.

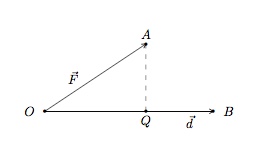
Le vecteur $\overrightarrow{F}$ est la somme des vecteurs $\overrightarrow{OQ}$ et $\overrightarrow{QA}$ où $\overrightarrow{QA}$ est orthogonal à $\overrightarrow{d}$.

Puisque $\overrightarrow{QA}$ ne contribue pas au déplacement horizontal, nous pouvons supposer que le mouvement de $O$ à $B$ est dû uniquement au vecteur $\overrightarrow{OQ}$. Le travail est donc le produit de $\|\overrightarrow{OQ}\| $ et de $\|\overrightarrow{d}\|$. Etant donné que $\overrightarrow{OQ}=\mbox{comp}_d\vec{F}$, en appliquant cette formule, nous obtenons

$$W=\dfrac{\vec{F}\odot\vec{d}}{\|\vec{d}\|}\|\vec{d}\|=\overrightarrow{F}\odot\overrightarrow{d}.$$

Le moment d'une force $\overrightarrow{F}$ appliquée en un point $A$, par rapport à un point $P$ est le produit vectoriel entre le vecteur position de cette force par rapport au point de référence et le vecteur force lui-même, soit

$$\overrightarrow{M}=\overrightarrow{PA}\times\overrightarrow{F}.$$

La projection orthogonale du vecteur position sur la perpendiculaire à la ligne d'action de la force est appelée bras de levier de la force et notée $\vec{d}$ avec

$$d=\Vert\vec{d}\Vert=\Vert\overrightarrow{PA}\Vert\, \sin{\alpha}.$$

Dans le cas particulier où le vecteur position $\overrightarrow{PA}$ est orthogonal à la force $\overrightarrow{F}$ la norme du moment est égale au produit des normes des deux vecteurs $\overrightarrow{PA}$ et $\overrightarrow{F}$.