LBARC 1143 Mathématique Géométrie Chapitre 8 : Les vecteurs Définitions et propriétés des vecteurs Exercices pour s'entraîner

Exercices pour s’entraîner

Entraînez-vous à résoudre les exercices suivants.

  1. Calculez $\|\overrightarrow{AB}\|$ ainsi que les coordonnées du point milieu de $\overrightarrow{AB}$ pour $A=(1,-4,5)$ et $B=(5,-2,3)$.

    Si $(x_a,y_a,z_a)$ et $(x_b,y_b,z_b)$ sont respectivement les coordonnées des points $A$ et $B$ alors,

    $\bullet\, $ le vecteur $\overrightarrow{AB}$ a pour composantes $(x_b-x_a,y_b-y_a,z_b-z_a)$

    $\bullet\, \|\overrightarrow{AB}\| =\sqrt{(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2}$

    $\bullet\, $ les coordonnées du point $M$, milieu du vecteur $\overrightarrow{AB}$ sont données par $\left(\frac{1}{2} (x_a + x_b),\frac{1}{2} (y_a+ y_b),\frac{1}{2} (z_a+ z_b)\right)$

    On a $\overrightarrow{AB}=(4,2,-2)$,  $\|\overrightarrow{AB}\|=\sqrt{16+4+4}=\sqrt{24}$ et $M=\frac{1}{2}(6,-6,8)=(3,-3,4)$.

  2. Déterminez $\vec{a}+\vec{b}$, $\vec{a}-\vec{b}$, $(\vec{a}-3\vec{b}$) pour $\vec{a}=(-2,6,1)$ et $\vec{b}=(3,-3,-1)$.

    Si $\vec{a}$ est le vecteur $(a_x,a_y,a_z)$ et $\vec{b}$ le vecteur $(b_x,b_y,b_z)$ alors

    $\bullet\, $ le vecteur somme est le vecteur $\overrightarrow{a+b}=(a_x+b_x,a_y+b_y,a_z+b_z)$

    $\bullet\, $ le vecteur $\overrightarrow{a-b}$ est donné par $\overrightarrow{a-b}=(a_x-b_x,a_y-b_y,a_z-b_z)$

    On a $\vec{a}+\vec{b}=(-2,6,1)+(3,-3,-1)=(1,3,0)$, $\vec{a}-\vec{b}=(-2,6,1)-(3,-3,-1)=(-5,9,2)$ et $\vec{a}-3\vec{b}=(-2,6,1)-3\cdot(3,-3,-1)=(-2,6,1)-(9,-9,-3)=(-11,15,4)$.

  3. Cherchez l'angle compris entre $\vec{a}$ et $\vec{b}$ pour $\vec{a}=(5,0,-1)$, $\vec{b}=(1,7,4)$

    Si $\theta$ désigne l'angle entre les deux vecteurs non nuls $\vec{u}$ et $\vec{v}$, alors $\cos\theta =\displaystyle\frac{\vec{u}\odot\vec{v}}{\|\vec{u}\|\|\vec{v}\|}$.

    On a $$ \begin{array}{rcl} \cos\theta & = & \dfrac{\vec{a}\odot\vec{b}}{\Vert\vec{a}\Vert\, \Vert\vec{b}\Vert}=\dfrac{5+0-4}{\sqrt{25+1}\, \sqrt{1+49+16}} \\ & = & \dfrac{1}{\sqrt{66}\, \sqrt{26}}=\dfrac{1}{\sqrt{1716}} \end{array} $$

    d'où $\theta=88,62^{\circ}$.

  4. Les vecteurs $\vec{a}$ et $\vec{b}$ sont-ils parallèles pour

    (a) $\vec{a}=(2,1,-5)$, $\vec{b}=(-6,-3,15)$

    (b) $\vec{a}=(-1,3,8)$, $\vec{b}=(2,-6,6)$

    Deux vecteurs sont parallèles s'ils sont multiples l'un de l'autre.

    (a) $\vec{a}$ et $\vec{b}$ sont parallèles car $\vec{b}=-3\vec{a}$.

    (b) $\vec{a}$ et $\vec{b}$ ne sont pas parallèles car on ne peut pas trouver $k\in\mathbb{R}$ tel que $\vec{b}=k\vec{a}$.

  5. Les vecteurs $\vec{a}$ et $\vec{b}$ sont-ils orthogonaux pour

    (a) $\vec{a}=(4,-1,-3)$, $\vec{b}=(2,1,1)$

    (b) $\vec{a}=(-3,2,1)$, $\vec{b}=(-4,-5,-2)$

    On a $\vec{u}\perp\vec{v}\Leftrightarrow\vec{u}\odot\vec{v}=0.$

    (a) $\vec{a}$ et $\vec{b}$ ne sont pas orthogonaux car $\vec{a}\odot\vec{b}=8-1-3=4\neq 0$.

    (b) $\vec{a}$ et $\vec{b}$ sont othogonaux car $\vec{a}\odot\vec{b}=(-3)\cdot (-4)+2\cdot (-5)+1\cdot(-2)=12-10-2=0$.

  6. Déterminez les valeurs de $c$ pour que les vecteurs $\vec{a}=(-4,2,-3)$ et $\vec{b}=(-1,22,c)$ soient orthogonaux

    On a $\vec{u}\perp\vec{v}\Leftrightarrow\vec{u}\odot\vec{v}=0.$

    Les vecteurs $\vec{a}$ et $\vec{b}$ sont othogonaux si $\vec{a}\odot\vec{b}=0$.

    On calcule $\vec{a}\odot\vec{b}=4+44-3c=0$ si $48-3c=0$ donc si $c=16$.

  7. Calculez le produit vectoriel des vecteurs $\vec a=(2,0,-1)$ et $\vec b=(-2,2,-1)$.  Donnez l'aire du parallélogramme construit sur $\vec a$ et $\vec b$.

    Soit $\vec{u}=(u_x,u_y,u_z)$ et $\vec{v}=(v_x,v_y,v_z)$. Les composantes du vecteur $\vec{u}\times\vec{v}$ sont données par

    $$\vec{u}\times\vec{v}=(u_yv_z-u_zv_y,u_zv_x-u_xv_z, u_xv_y-u_yv_x).$$

    La longueur $\|\vec{u}\times\vec{v}\|$ est l'aire du parallélogramme construit sur les vecteurs $\vec{u}$ et $\vec{v}$.

    On calcule $\vec a\times\vec b=(0\cdot(-1)-(-1)\cdot 2,(-1)\cdot(-2)-2\cdot(-1),2\cdot 2-(-2)\cdot0)=(2,4,4)$.

    L'aire du parallélogramme est donnée par $\Vert\vec a\times\vec b\Vert=\Vert(2,4,4)\Vert=\sqrt{4+16+16}=\sqrt{36}=6.$

  8. Le point $P$ est soumis à deux forces $\overrightarrow{PQ}$ et $\overrightarrow{PR}$ d'intensités respectives de 4N et 6N. La direction de $\overrightarrow{PQ}$ est N$30^\circ$W et la direction de $\overrightarrow{PR}$ est S$60^\circ$W. Donnez les composantes horizontales et verticales de $\overrightarrow{PQ}$ et $\overrightarrow{PR}$.  Calculez la résultante de ces deux forces.

    Soit $\vec v$ un vecteur formant un angles $\theta$ avec l'axe $OX$.

    La composante horizontale de $\vec v$ est $\Vert\vec v\Vert\, \cos\, \theta$ et la composante verticale de $\vec v$ est $\Vert\vec v\Vert\, \sin\, \theta$.

    La résultante de deux forces est leur somme.

    On a $\overrightarrow{PQ}=(4\, \cos 120^\circ,4\, \sin 120^\circ)=(-2,2\sqrt{3})$ et $\overrightarrow{PR}=(6\, \cos 210^\circ,6\, \sin 210^\circ)=(-3\sqrt{3},-3)$.

    La résultante est donnée par le vecteur $\overrightarrow{PQ}+\overrightarrow{PR}=(-2,2\sqrt{3})+(-3\sqrt{3},-3)=(-2-3\sqrt{3},-3+2\sqrt{3})$.

  9. Pour placer une caisse de 75kg sur un camion, on la soulève à l'aide de deux câbles passant sur des poulies sans frottement. Ces câbles forment des angles de $60^{\circ}$ et $30^{\circ}$ avec l'horizontale. Déterminez les efforts dans les deux câbles.

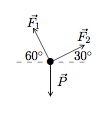
    Ecrivez les différentes forces sous forme de vecteurs et exprimez que le système est à l'équilibre, c'est-à-dire que la somme des forces est nulle.

    Vu que $75$ kg $\approx 750$ N, on a $\vec{P}=(0,-750)$. De plus,

    $$\vec{F_1}=(-\Vert\vec{F_1}\Vert\cos{60^{\circ}},\Vert\vec{F_1}\Vert\sin{60^{\circ}})=(-\frac{1}{2}\Vert\vec{F_1}\Vert,\frac{\sqrt{3}}{2}\Vert\vec{F_1}\Vert),$$

    et

    $$\vec{F_2}=(\Vert\vec{F_2}\Vert\cos{30^{\circ}},\Vert\vec{F_2}\Vert\sin{30^{\circ}})=(\frac{\sqrt{3}}{2}\Vert\vec{F_2}\Vert,\frac{1}{2}\Vert\vec{F_2}\Vert).$$

    Pour que le système soit en équilibre, il faut que la somme des composantes verticales et horizontales des forces en jeu soit nulle, c'est-à-dire

    $$-\frac{1}{2}\Vert\vec{F_1}\Vert+\frac{\sqrt{3}}{2}\Vert\vec{F_2}\Vert+0=0$$

    et

    $$\frac{\sqrt{3}}{2}\Vert\vec{F_1}\Vert+\frac{1}{2}\Vert\vec{F_2}\Vert-750=0.$$

    On en déduit $$ \left\{ \begin{array}{l} \Vert\vec{F_1}\Vert=\sqrt{3}\Vert\vec{F_2}\Vert\\ \frac{\sqrt{3}}{2}\, \sqrt{3}\Vert\vec{F_2}\Vert+\frac{1}{2}\Vert\vec{F_2}\Vert-750=0 \end{array} \right. $$

    d'où $\Vert\vec{F_2}\Vert=375$ N et $\Vert\vec{F_1}\Vert=375\sqrt{3}$ N.

  10. En utilisant le produit vectoriel, montrez que les vecteurs $\vec{u}=(1,-2,3)$ et $\vec{v}=(-2,4,-6)$ sont parallèles.

    On a $\vec{u}\parallel\vec{v}\Leftrightarrow\vec{u}\times\vec{v}=\vec o.$

    Les composantes du vecteur $\vec{u}\times\vec{v}$ sont données par cette formule.

    On a

    $$\vec{u}\times\vec{v}=(-2\cdot (-6)-3\cdot 4,3\cdot (-2)-(-6)\cdot 1, 1\cdot 4-(-2)\cdot (-2))=(0,0,0)=\vec{o}.$$

    et donc les vecteurs sont parallèles. De plus, $\vec{v}=-2\vec{u}$.