Exercices résolus
Voici quelques exemples d'exercices résolus en détails.
-
Quelle est la norme des vecteurs $(-5,6)$ et $(3,-2,1)$ ?
La norme d'un vecteur est donnée par cette fomule.
On a $$\Vert (-5,6)\Vert=\sqrt{(-5)^2+6^2}=\sqrt{25+36}=\sqrt{61}$$
et $$\Vert (3,-2,1)\Vert=\sqrt{3^2+(-2)^2+1^2}=\sqrt{9+4+1}=\sqrt{14}.$$
-
Si le vent souffle à 20km/h dans la direction S$45^\circ$E, exprimer sa vitesse par un vecteur $\vec{v}$.
On a $\vec{v}=(20\cos{315^\circ}, 20\sin{315^\circ})=(20\cdot\frac{\sqrt{2}}{2},-20\cdot\frac{\sqrt{2}}{2})=(10\sqrt{2},-10\sqrt{2})$.
-
Quel est l'opposé du vecteur $(-3,8,-1)$ ?
L'opposé du vecteur $(-3,8,-1)$ est le vecteur $-(-3,8,-1)=(3,-8,1)$.
-
Donnez les composantes du vecteur $\vec{u}\times\vec{v}$ si $\vec{u}=(1,3,2)$ et $\vec{v}=(4,-1,-2)$.
Les composantes du vecteur $\vec{u}\times\vec{v}$ sont données par cette formule.
On a $\vec{u}\times\vec{v}=(3\cdot (-2)-2\cdot (-1),2\cdot 4-1\cdot (-2),1\cdot (-1)-3\cdot 4)=(-4,10,-13)$.
-
Donnez un vecteur orthogonal aux vecteurs $(1,0,-2)$ et $(2,-3,4)$ ainsi que l'aire du parallélogramme construit sur ces deux vecteurs.
Un vecteur orthogonal à deux autres est leur produit vectoriel de ces deux vecteurs. Les composantes du vecteur $\vec{u}\times\vec{v}$ sont données par cette formule.
On obtient $(0\cdot 4-(-2)\cdot(-3),(-2)\cdot2-1\cdot4,1\cdot(-3)-0\cdot2)=(-6,-8,-3)$.
L'aire du parallélogramme construit sur ces deux vecteurs est la norme de leur produit vectoriel $\Vert(-6,-8,-3)\Vert=\sqrt{(-6)^2+(-8)^2+(-3)^2}=\sqrt{36+64+9}=\sqrt{109}$.
-
Les vecteurs $(2,-4,6)$ et $(-1,2,-3)$ sont-ils colinéaires ?
Les vecteurs sont colinéaires car $(2,-4,6)=-2(-1,2,-3)$.
-
Dans le parallélipipède rectangle ci-dessous, déterminez les coordonnées de tous les sommets. Calculez ensuite le volume de ce parallélipipède.
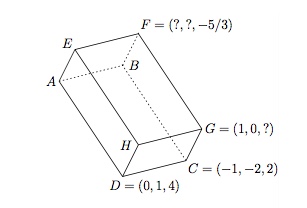
Soit $G=(1,0,z)$. On a $\overrightarrow{CG}\perp\overrightarrow{CD}$ et donc
$$\overrightarrow{CG}\odot\overrightarrow{CD}=(2,2,z-2)\odot(1,3,2)=0.$$
On en déduit $2+6+2z-4=2z+4=0$ d'où $z=-2$ et $G=(1,0,-2)$.
Soit $F=(x,y,-\frac{5}{3})$. On a $\overrightarrow{GF}\perp\overrightarrow{CG}$ et $\overrightarrow{GF}\perp\overrightarrow{CD}$ donc $\overrightarrow{GF}=k(\overrightarrow{CG}\times\overrightarrow{CD})$. Vu que
$$\overrightarrow{CG}\times\overrightarrow{CD}=(16,-8,4),$$
on a $\overrightarrow{GF}=(x-1,y,-\frac{5}{3}+2)=k(16,-8,4)$. On en déduit $k=\frac{1}{12}$ et donc $F=(\frac{7}{3},-\frac{2}{3},-\frac{5}{3})$.
Soit $E=(x,y,z)$. On a $\overrightarrow{FE}=\overrightarrow{CD}$ d'où $\overrightarrow{FE}=(x-\frac{7}{3},y+\frac{2}{3},z+\frac{5}{3})=(1,3,2).$
On en déduit $E=(\frac{10}{3},\frac{7}{3},\frac{1}{3})$.
Soit $A=(x,y,z)$. On a $\overrightarrow{EA}=\overrightarrow{GC}$ d'où $\overrightarrow{EA}=(x-\frac{10}{3},y-\frac{7}{3},z-\frac{1}{3})=(-2,-2,4).$
On en déduit $A=(\frac{4}{3},\frac{1}{3},\frac{13}{3})$.
Soit $B=(x,y,z)$. On a $\overrightarrow{AB}=\overrightarrow{DC}$ d'où $\overrightarrow{AB}=(x-\frac{4}{3},y-\frac{1}{3},z-\frac{13}{3})=(-1,-3,-2).$
On en déduit $B=(\frac{1}{3},-\frac{8}{3},\frac{7}{3})$.
Soit $H=(x,y,z)$. On a $\overrightarrow{DH}=\overrightarrow{CG}$ d'où $\overrightarrow{DH}=(x,y-1,z-4)=(2,2,-4).$
On en déduit $H=(2,3,0)$.
Le volume du parallélipipède construit sur les vecteurs $\overrightarrow{CG}$, $\overrightarrow{CD}$ et $\overrightarrow{GF}$ est donné par
$$V=|(\overrightarrow{CG}\times\overrightarrow{CD})\odot\overrightarrow{GF}|.$$
On a vu que $\overrightarrow{CG}\times\overrightarrow{CD}=(16,-8,4)$ et $\overrightarrow{GF}=(\frac{4}{3},-\frac{2}{3},\frac{1}{3})$, donc le volume est
$$V=\left|(16,-8,4)\odot\left(\frac{4}{3},-\frac{2}{3},\frac{1}{3}\right)\right|=\left|\frac{64}{3}+\frac{16}{3}+\frac{4}{3}\right|=\frac{84}{3}=28.$$