LBARC 1143 Mathématique Géométrie Anciens Examens Examen de Mai 2016

Examen de Mai 2016

Pour vous tester, essayez de résoudre cet ancien examen.

Imprimer en PDF
1

Enoncez et démontrez le Théorème de Pythagore.

Enoncé : Dans un triangle rectangle, le carré de la longueur de l'hypothénuse est égal à la somme des carrés des longueurs des deux autres côtés.

Démonstration : On considère le triangle rectangle

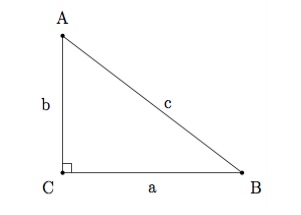
Construisons un carré de côté $a+b$ et décomposons-le de deux manières différentes :

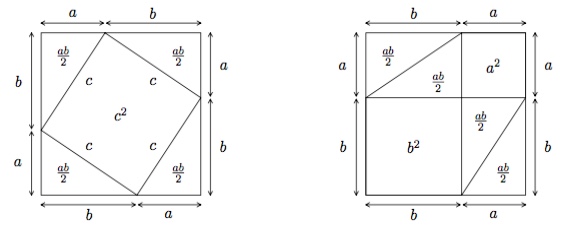
L'aire du premier carré est égale à $$c^2+4\dfrac{ab}{2}=c^2+2ab.$$

Celle du deuxième carré est égale à $$a^2+b^ 2+4\dfrac{ab}{2}=a^2+b^ 2+2ab.$$

Puisque les deux aires sont égales, on obtient $a^2+b^2=c^2$.

2

Montrez que dans un cercle, un diamètre perpendiculaire à une corde divise celle-ci en 2 parties égales.

Soit $r$ le rayon du cercle, $AB$ la corde et $OX$ le diamètre tel que $AB\perp OX$.

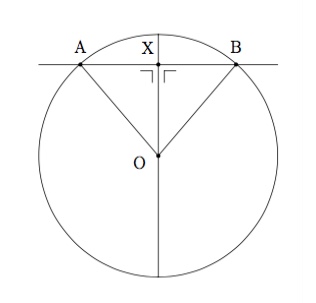
Il faut voir que $\vert AX\vert=\vert XB\vert$.

Par Pythagore dans le triangle $AXO$, on a $$\vert AX\vert^2=\vert OA\vert^2-\vert XO\vert^2.$$

Par Pythagore dans le triangle $BXO$, on a $$\vert XO\vert^2=\vert OB\vert^2-\vert XB\vert^2.$$

On en déduit $$ \begin{array}{rcl} \vert AX\vert^2&=&\vert OA\vert^2-\vert XO\vert^2\\ &=&\vert OA\vert^2-(\vert OB\vert^2-\vert XB\vert^2)\\ &=&\vert OA\vert^2-\vert OB\vert^2+\vert XB\vert^2\\ &=&r^2-r^2+\vert XB\vert^2\\ &=&\vert XB\vert^2 \end{array} $$
et donc $\vert AX\vert=\vert XB\vert$.

3

Voici la photo d'un pont à Venise. Ce pont est de forme parabolique et ses dimensions sont données dans le schéma ci-dessous.

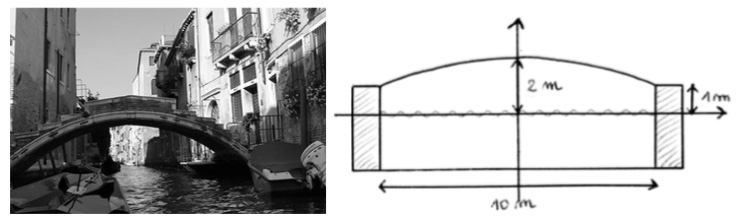
  1. Déterminez l'équation du pont dans le repère proposé (où l'axe des abscisses correspond au niveau de l'eau).

    Soit $P\, :\, y=ax^2+bx+c$ l'équation de la parabole.

    Puisque le sommet se trouve au point $(0,2)$, on a $c=2$ et $\dfrac{-b}{2a}=0$.

    De plus, le point $(5,1)\in P$ et donc $1=25a+5b+c$.

    Il faut donc résoudre le système $$ \left\{ \begin{array}{l} c=2\\ \dfrac{-b}{2a}=0\\ 1=25a+5b+c \end{array} \right. $$

    On trouve $c=2$, $b=0$ et $a=-\frac{1}{25}$. La parabole cherchée a donc pour équation $$y=-\frac{1}{25}x^2+2.$$

  2. Une gondole s'aventure sous le pont à $3$ mètres de la berge. En supposant que le plancher du bateau s'enfonce de $5$ cm en-dessous du niveau de l'eau, déterminez la taille maximale du gondolier pour qu'il puisse passer sous le pont sans se baisser.

    Il faut trouver $y$ correspondant à $x=2$ : $$y=-\dfrac{4}{25}+2=\dfrac{46}{25}=1,84.$$

    Vu que le bateau s'enfonce de $5$ cm, la taille maximale du gondolier est $1,84+0,05=1,89$ m.
4

On considère le parallélipipède rectangle ci-dessous. Déterminez les coordonnées des sommets $C$, $G$ et $H$ ainsi que le volume de ce parallélipipède.

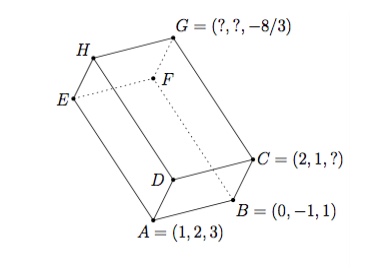
  • Soit $C=(2,1,z)$. On a $\overrightarrow{AB}\perp\overrightarrow{BC}$ et donc $$\overrightarrow{AB}\odot\overrightarrow{BC}=(-1,-3,-2)\odot(2,2,z-1)=0.$$

On en déduit $-2-6-2z+2=0$ d'où $z=-3$ et $C=(2,1,-3)$.

  • Soit $G=(x,y,-\frac{8}{3})$. On a $\overrightarrow{CG}\perp$ plan $ABC$ donc $\overrightarrow{CG}=k\vec{n}$ où $\vec{n}$ est le vecteur normal au plan. Vu que $$\vec{n}=\overrightarrow{AB}\times\overrightarrow{BC}=(-1,-3,-2)\times (2,2,-4)=(16,-8,4),$$

on a $\overrightarrow{CG}=(x-2,y-1,-\frac{8}{3}+3)=k(16,-8,4)$. On en déduit $k=\frac{1}{12}$ et donc $G=\left(\dfrac{10}{3},\dfrac{1}{3},-\dfrac{8}{3}\right)$.

  • Soit $H=(x,y,z)$. On a $\overrightarrow{GH}=\overrightarrow{BA}$ d'où $$\overrightarrow{GH}=\left(x-\frac{10}{3},y-\frac{1}{3},z+\frac{8}{3}\right)=(1,3,2).$$

On en déduit $H=\left(\dfrac{13}{3},\dfrac{10}{3},-\dfrac{2}{3}\right)$.

  • Le volume du parallélipipède construit sur les vecteurs $\overrightarrow{AB}$, $\overrightarrow{BC}$ et $\overrightarrow{CG}$ est donné par $V=\Vert\overrightarrow{AB}\Vert\cdot \Vert\overrightarrow{BC}\Vert\cdot \Vert\overrightarrow{CG}\Vert$ et donc $$V=\sqrt{1+9+4}\cdot \sqrt{4+4+16}\cdot \sqrt{\frac{16}{9}+\frac{4}{9}+\frac{1}{9}}=\sqrt{14\cdot 24\cdot\frac{21}{9}}=\sqrt{784}=28.$$
5

Donnez les solutions de l'équation $\cos{x}=-\sin{\frac{x}{2}}$ dans $[0,2\pi]$.

L'équation peut encore s'écrire $$\cos{x}=\sin{\left(-\frac{x}{2}\right)}$$

$$\cos{x}=\cos{\left(\frac{\pi}{2}+\frac{x}{2}\right)}$$

On en déduit

  • $x=\frac{\pi}{2}+\frac{x}{2}+2k\pi$ et donc $x=\pi+4k\pi$ avec $k\in\mathbb{Z}$,
  • $x=-(\frac{\pi}{2}+\frac{x}{2})+2k\pi$ et donc $x=-\frac{\pi}{3}+\frac{4k\pi}{3}$ avec $k\in\mathbb{Z}$.

Parmi ces solutions, la seule à être dans $[0,2\pi]$ est $x=\pi$.

6

On considère la droite $$ \Delta\, :\, \left\{ \begin{array}{l} x+y+2z=5\\ x-z=-2 \end{array} \right. $$

  1. Donnez un point et un vecteur directeur de la droite $\Delta$.

    Le point $Q=(1,-2,3)$ est un point de la droite $\Delta$.

    Soit $\vec{n_1}=(1,1,2)$ un vecteur normal au plan $x+y+2z=5$ et $\vec{n_2}=(1,0,-1)$ un vecteur normal au plan $x-z=-2$. Alors le vecteur $\vec{v}=\vec{n_1}\times\vec{n_2}=(-1,3,-1)$ est un vecteur directeur de la droite $\Delta$.

  2. Déterminez l'équation du plan $\Pi$ qui passe par le point $P=(1,1,1)$ et la droite $\Delta$.

    Le plan $\Pi$ contient les points $P$ et $Q$. Son vecteur normal est donc orthogonal au vecteur $\overrightarrow{PQ}=(0,-3,2)$. De plus, le plan $\Pi$ contient la droite $\Delta$. Son vecteur normal est donc orthogonal au vecteur directeur de la droite $\vec{v}=(-1,3,-1)$. On en déduit que le vecteur $\vec{n}=\vec{v}\times\overrightarrow{PQ}=(3,2,3)$ est un vecteur normal au plan $\Pi$. Le plan $\Pi$ a donc pour équation $$3x+2y+3z=3+2+3$$ c'est-à-dire$$3x+2y+3z=8.$$
7

Ecrivez la réponse correcte dans la case à la fin de la phrase sans justifier.

  1. Donnez l'équation du cercle centré en $(-2,3)$ et de rayon $5$.

    La formule pour trouver l'équation d'un cercle se trouve ici.  On obtient $(x+2)^2+(y-3)^2=25$.

  2. Donnez l'équation de la médiatrice du segment joignant les points $(4,3)$ et $(-2,5)$.

    La médiatrice du segment a pour équation $y=3x+1$.

  3. Calculez l'aire du parallélogramme construit sur les vecteurs $(1,0,2)$ et $(-1,2,1)$.

    L'aire du parallélogramme construit sur les vecteurs $(1,0,2)$ et $(-1,2,1)$ est donnée par $\Vert (1,0,2)\times (-1,2,1)\Vert=\sqrt{29}$.

  4. Si on double le rayon d'un cône circulaire et on divise par $4$ sa hauteur, par combien est multiplié son volume ?

    Son volue ne change pas.  Il est donc multiplié par $1$.

  5. $\alpha$ est un angle du quatrième quadrant dont le cosinus vaut $\frac{3}{4}$. Déterminez $\sin{\alpha}$.

    On a $\sin^2{\alpha}=1-\cos^2{\alpha}=1-\frac{9}{16}=\frac{7}{16}$.  On en déduit $\sin{\alpha}=\pm\frac{\sqrt{7}}{4}$ et comme $\alpha$ est un angle du quatrième quadrant son sinus est négatif.  Finalement $\sin{\alpha}=-\frac{\sqrt{7}}{4}$.
8

Les propositions suivantes sont-elles vraies ou fausses ? Répondez par V ou F dans la case à la fin de la phrase, sans justifier. Une mauvaise réponse entraînera l'annulation d'une bonne réponse. Vous pouvez vous abstenir sans être pénalisé.

  1. Les vecteurs $(0,4,-4)$ et $(1,-2,2)$ sont orthogonaux.

    Faux.  On a $(0,4,-4)\odot (1,-2,2)=-8-8=-16\neq 0$ et donc les vecteurs ne sont pas orthogonaux.

  2. Pour tout $x\in\mathbb{R}$, on a $\sin{x}=\cos{(\frac{\pi}{2}+x)}$.

    Faux.  Pour tout $x\in\mathbb{R}$, on a $\sin{x}=\cos{(\frac{\pi}{2}-x)}$.

  3. Dans $\mathbb{R}^2$, si deux droites sont perpendiculaires alors le produit de leurs pentes vaut $0$.

    Faux. Dans $\mathbb{R}^2$, si deux droites sont perpendiculaires alors le produit de leurs pentes vaut $-1$.

  4. Si un plan contient une droite alors le vecteur normal au plan est un multiple du vecteur directeur de la droite.

    Faux.  Si un plan contient une droite alors le vecteur normal au plan est orthogonal au vecteur directeur de la droite.

  5. Dans un triangle rectangle, l'orthocentre et le centre de gravité sont les mêmes.

    Faux. Dans tout triangle, l'orthocentre et le centre de gravité sont alignés.