Questions de théorie
Ces questions sont destinées à vous faire revoir la théorie de ce chapitre.
Définissez un cercle, des cercles concentriques, le diamètre d'un cercle.
Les définitions et des illustrations se trouvent dans le syllabus, chapitre 5, section 1.1.
Soit $C$ un point du plan et $r>0$.
Le cercle de centre $C$ et de rayon $r$ est l'ensemble des points du plan situés à distance $r$ du point $C$.
On dira que des cercles sont concentriques s'ils ont le même centre.
Le diamètre d'un cercle est un segment qui passe par son centre et a pour extrémités deux points du cercle.
Définissez un arc de cercle et une corde.
Les définitions et des illustrations se trouvent dans le syllabus, chapitre 5, section 1.1.
Soit $P$ et $Q$ deux points d'un cercle.
L'arc de cercle $PQ$ est la partie du cercle délimitée par les points $P$ et $Q$.
La corde $[PQ]$ est le segment joignant $P$ à $Q$.
Donnez la longueur de l'arc intercepté par un angle $\alpha$ sur un cercle de rayon $r$.
La définition et une illustration se trouvent dans le syllabus, chapitre 5, section 1.3.
La longueur de l'arc intercepté par un angle $\alpha$ sur un cercle de rayon $r$ est donnée par $L=r\alpha$, où $\alpha$ est mesuré en radians.
Définissez et donnez la surface d'un secteur circulaire.
La définition et une illustration se trouvent dans le syllabus, chapitre 5, section 1.3.
On appelle secteur circulaire la portion de disque comprise entre un arc et les 2 rayons qui aboutissent à ses extrémités.
La surface du secteur circulaire de rayon $r$ et d'angle $\alpha$ est le nombre $S=\dfrac{r^2\alpha}{2}$, où $\alpha$ est mesuré en radians.
Définissez et donnez la surface d'un segment circulaire.
La définition et une illustration se trouvent dans le syllabus, chapitre 5, section 1.3.
On appelle segment circulaire la portion de disque comprise entre un arc et la corde qui le sous-tend.
Un segment circulaire a pour surface le nombre $$ S=\dfrac{r^2}{2}(\alpha-\sin\alpha), $$
où $\alpha$ est mesuré en radians.
Précisez les positions relatives de deux cercles en fonction de leurs rayons.
Les définitions et illustrations se trouvent dans le syllabus, chapitre 5, section 1.2.
Soit $C_1$ le cercle de centre $O_1$ et de rayon $r_1$ et $C_2$ le cercle de centre $O_2$ et de rayon $r_2$ avec $r_1>r_2$. Notons $d$ la distance entre $O_1$ et $O_2$.
Si $d>r_1+r_2$ alors les cercles sont extérieurs.
Si $d=r_1+r_2$ alors les cercles sont tangents extérieurement.
Si $r_1-r_2<d<r_1+r_2$ alors les cercles sont sécants.
Si $d=r_1-r_2$ alors les cercles sont tangents intérieurement.
Si $d<r_1-r_2$ alors les cercles sont intérieurs.
Si $d=0$ alors les cercles sont concentriques.
Définissez un polygone, un polygone régulier, un polygone convexe.
Les définitions se trouvent dans le syllabus, chapitre 5, section 2.
Un polygone est une figure plane délimitée par une ligne fermée constituée de segments de droite. Ces segments sont les côtés du polygone et le point d'intersection de deux côtés est appelé sommet du polygône.
Un polygône est régulier si tous ses côtés ont même longueur et tous ses angles intérieurs ont même amplitude.
Un polygône est convexe si tout segment ayant ses extrémités sur le polygône y est inclus tout entier.
Définissez un cercle circonscrit à un polygone régulier.
La définition se trouve dans le syllabus, chapitre 5, section 2.
Si le polygône régulier a un nombre impair de côtés, toute droite joignant un sommet au milieu du côté opposé est un axe de symétrie. Si le polygône a un nombre pair de côtés, toute droite joignant un sommet au sommet opposé est un axe de symétrie et toute droite joignant le milieu de deux côtés opposés est aussi un axe de symétrie.
Tous les axes de symétrie d'un polygône régulier se coupent en un point qui est le centre d'un cercle dans lequel on peut inscrire le polygône. Le cercle circonscrit au polygône est le cercle centré en ce point et passant par tous les sommets du polygône.
Que vaut la somme des mesures des angles dans un polygone ? et en particulier dans un triangle ?
La propriété se trouve dans le syllabus, chapitre 5, section 2.
La somme des mesures des angles d'un polygône à $n$ côtés vaut $(n-2)\times 180^{\circ}$.
Dans le cas d'un triangle, $n=3$ et donc la somme des mesures des angles d'un triangle vaut $180^{\circ}$.
Enoncez un résultat concernant la droite parallèle au milieu des côtés d'un triangle.
La propriété se trouve dans le syllabus, chapitre 5, section 2.
Dans tout triangle, la droite passant par le milieu d'un côté et parallèle à un autre côté coupe le troisième côté en son milieu.
Réciproquement, dans tout triangle, le segment joignant les milieux de deux des côtés est parallèle au troisième côté et sa longueur vaut la moitié de celle de ce troisième côté.
Donnez la surface d'un triangle de 5 manières différentes.
Les formules se trouvent dans le syllabus, chapitre 5, section 2.
La surface $S$ du triangle de côtés $a$, $b$, $c$ est donnée par
(a) $S=\dfrac{ch}{2}$ où $h$ est la hauteur perpendiculaire à $c$;
(b) $S=\dfrac{bc\sin{\alpha}}{2}$ où $\alpha$ est l'angle entre les côtés $b$ et $c$;
(c) $S=\dfrac{r(a+b+c)}{2}=\dfrac{rP}{2}$ où $P$ est le périmètre et $r$ est le rayon du cercle inscrit;
(d) $S=\dfrac{\sqrt{P(P-2a)(P-2b)(P-2c)}}{4}$ où $P$ est le périmètre (Formule de Héron);
(e) $S=\dfrac{abc}{4R}$ où $R$ est le rayon du cercle circonscrit.
Démontrez la formule de la surface d'un triangle de côtés $a$, $b$, $c$ si on connaît la hauteur $h$ relative au côté $c$.
La démonstration se trouve dans le syllabus, chapitre 5, section 2.
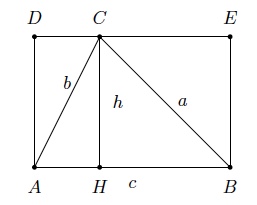
Les triangles $ADC$ et $AHC$ sont égaux et les triangle $BCE$ et $BHC$ sont égaux.
On en déduit que aire($ABC$)=$\frac{1}{2}$(aire($ABED$)) et donc $$ S=\dfrac{ch}{2} $$
où $h$ est la hauteur perpendiculaire à $c$.
Démontrez la formule de la surface d'un triangle de côtés $a$, $b$, $c$ si on connaît l'angle $\alpha$ entre les côtés $b$ et $c$.
La démonstration se trouve dans le syllabus, chapitre 5, section 2.
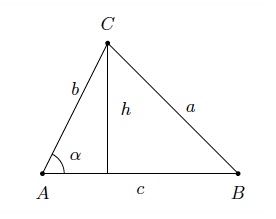
Vu que que $S=\dfrac{ch}{2}$ et $h=b\sin{\alpha}$, on a $$ S=\dfrac{bc\sin{\alpha}}{2} $$
où $\alpha$ est l'angle entre les côtés $b$ et $c$.
Démontrez la formule de la surface d'un triangle de côtés $a$, $b$, $c$ si on connaît le périmètre et le rayon du cercle inscrit.
La démonstration se trouve dans le syllabus, chapitre 5, section 2.
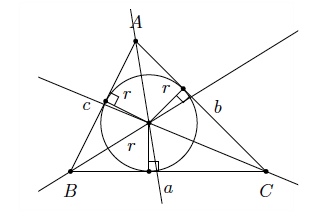
Le centre du cercle inscrit est l'intersection des bissectrices. On a $$ \begin{array}{rcl} S & = & S_1+S_2+S_3 \\[2mm] & = & \dfrac{cr}{2}+\dfrac{br}{2}+\dfrac{ar}{2} \\[2mm] & = & \dfrac{r}{2}(a+b+c) \\ & = & \dfrac{rP}{2} \end{array} $$où $P$ est le périmètre et $r$ est le rayon du cercle inscrit.
Démontrez la formule de la surface d'un triangle de côtés $a$, $b$, $c$ si on connaît le rayon du cercle circonscrit.
La démonstration se trouve dans le syllabus, chapitre 5, section 2.
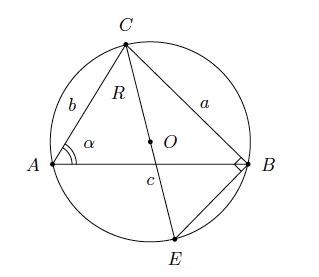
Le centre du cercle circonscrit est l'intersection des médiatrices.
Soit $O$ le centre du cercle circonscrit et $E$ l'intersection de la droite $OC$ avec le cercle.
Le triangle $BEC$ est rectangle en $B$.
De plus, $\widehat{E}=\widehat{A}$ car ils sous-tendent le même arc $BC$.
On en déduit que $\widehat{E}=\alpha$ et $\sin{\alpha}=\dfrac{a}{2R}$.
Donc puisque $S=\dfrac{bc\sin\alpha}{2}$ on a $$ S=\dfrac{bc}{2}\cdot\dfrac{a}{2R}=\dfrac{abc}{4R} $$
où $R$ est le rayon du cercle circonscrit.
Enoncez la Formule de Héron.
La formule se trouve dans le syllabus, chapitre 5, section 2.
Formule de Héron : $S=\dfrac{\sqrt{P(P-2a)(P-2b)(P-2c)}}{4}$ où $P$ est le périmètre du triangle.
Cette formule permet de calculer l'aire d'un triangle en connaissant la longueur de ses trois côtés.
Expliquez comment calculer l'aire d'un terrain de forme polygonale.
L'explication se trouve dans le syllabus, chapitre 5, section 2.
La Formule de Héron permet de calculer l'aire d'un triangle en connaissant la longueur de ses trois côtés.
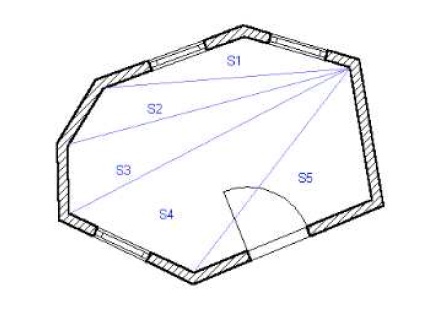
Elle permettra aussi de calculer l'aire d'une pièce ou d'un terrain de forme polygonale. En effet, il suffira de trianguler la pièce (découper la pièce en triangles), de calculer l'aire de chacun des triangles en mesurant les côtés et d'additionner toutes les aires pour obtenir l'aire totale.
Définissez médiane et diagonale d'un quadrilatère.
Les définitions se trouvent dans le syllabus, chapitre 5, section 2.
Une diagonale d'un quadrilatère est un segment de droite qui relie deux sommets opposés. Une médiane d'un quadrilatère est un segment de droite qui relie les milieux de deux côtés opposés.
Définissez trapèze, parallélogramme, rectangle, losange et carré et donnez leurs propriétés.
Les définitions et des illustrations se trouvent dans le syllabus, chapitre 5, section 2.
Un trapèze est un quadrilatère qui a deux côtés opposés parallèles. Ces côtés parallèles sont appelés les bases du trapèze. Un trapèze qui possède un angle droit est un trapèze rectangle. Un trapèze dont les deux côtés non parallèles ont même longueur est un trapèze isocèle.
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles. Les côtés opposés d'un parallélogramme ont même longueur et ses angles opposés ont même amplitude.
Un losange est un quadrilatère qui possède quatre côtés de même longueur.
Un rectangle est un quadrilatère qui a quatre angles droits.
Un carré est un quadrilatère qui a quatre côtés de même longueur et quatre angles droits.
Donnez le périmètre et la surface d'un carré, rectangle, parallélogramme, losange et trapèze.
Les formules se trouvent dans le syllabus, chapitre 5, section 2.
Le carré de côté $c$ a pour périmètre le nombre $P=4c$ et sa surface est le nombre $S=c^2$.
Le rectangle de longueur $L$ et de largeur $l$ a pour périmètre le nombre $P=2(L+l)$ et sa surface est le nombre $S=Ll$.
Le périmètre d'un parallélogramme de côtés non parallèles $B$ et $b$ est le nombre $P=2(B+b)$. La surface du parallélogramme de base $B$ et de hauteur $h$ est le nombre $S=Bh$.
Le losange de grande diagonale $D$ et de petite diagonale $d$ a pour périmètre le nombre $P=2\sqrt{D^2+d^2}$ et sa surface est le nombre $S=\dfrac{Dd}{2}$.
Le trapèze de grande base $B$, de petite base $b$ et de hauteur $h$ a pour surface le nombre $S=\frac{1}{2}(B+b)h$. Pour trouver son périmètre, il faut additionner la longueur de ses quatre côtés.
Donnez les propriétés des médianes et des diagonales d'un carré.
Les propriétés se trouvent dans le syllabus, chapitre 5, section 2.
Les diagonales d'un carré sont perpendiculaires, se coupent en leur milieu et ont même longueur.
Les médianes d'un carré sont perpendiculaires, se coupent en leur milieu et ont même longueur.
Les médianes d'un carré sont parallèles aux côtés.
Les diagonales et les médianes d'un carré se coupent en un même point.
Donnez les propriétés des médianes et des diagonales d'un rectangle.
Les propriétés se trouvent dans le syllabus, chapitre 5, section 2.
Les diagonales d'un rectangle ont même longueur et se coupent en leur milieu.
Les médianes d'un rectangle sont perpendiculaires et se coupent en leur milieu.
Les médianes d'un rectangle sont parallèles aux côtés.
Les diagonales et les médianes d'un rectangle se coupent en un même point, centre du cercle circonscrit au rectangle.
Donnez les propriétés des médianes et des diagonales d'un parallélogramme.
Les propriétés se trouvent dans le syllabus, chapitre 5, section 2.
Les diagonales d'un parallélogramme se coupent en leur milieu.
Les médianes d'un parallélogramme se coupent en leur milieu.
Les médianes d'un parallélogramme sont parallèles aux côtés.
Les diagonales et les médianes d'un parallélogramme se coupent en un même point.
Donnez les propriétés des médianes et des diagonales d'un losange.
Les propriétés se trouvent dans le syllabus, chapitre 5, section 2.
Les diagonales d'un losange sont perpendiculaires et se coupent en leur milieu.
Les médianes d'un losange ont même longueur et se coupent en leur milieu.
Les médianes d'un losange sont parallèles aux côtés.
Les diagonales et les médianes d'un losange se coupent en un même point.
Construisez géométriquement le nombre d'or.
La construction se trouve dans le syllabus, chapitre 5, section 2.
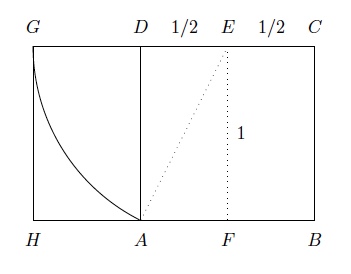
Pour construire graphiquement le nombre d'or : on prend un carré $ABCD$ de côté $1$ et $E$ le milieu de $CD$. On trace le cercle de centre $E$ et de rayon $EA$.
Le segment $GC$ est de longueur $\phi$.
En effet, $r=|EA|=\sqrt{1+\frac{1}{4}}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2}$ et donc $$ |GC|=|GE|+|EC|=|EA|+\dfrac{1}{2}=\dfrac{\sqrt{5}}{2}+\dfrac{1}{2}=\dfrac{\sqrt{5}+1}{2}=\phi. $$