Questions de théorie

On appelle vecteur une quantité caractérisée par une longueur (ou intensité), par une direction et par un sens dans cette direction.

Considérons un repère cartésien orthonormé. En plaçant l'origine du vecteur $\vec{v}$ à l'origine du repère, on obtient le point $V$ qui est l'extrémité de $\vec{v}$. On a donc $\vec{v}=\overrightarrow{OV}$. Le point $V$ est un point du plan ou de l'espace et a donc des coordonnées cartésiennes. Les composantes du vecteur $\vec{v}$ sont les coordonnées du point $V$.

• Dans le plan, si $(x_a,y_a)$ et $(x_b,y_b)$ sont respectivement les coordonnées des points $A$ et $B$, le vecteur $\overrightarrow{AB}$ a pour composantes $(x_b-x_a,y_b-y_a)$.

• Dans l'espace, si $(x_a,y_a,z_a)$ et $(x_b,y_b,z_b)$ sont respectivement les coordonnées des points $A$ et $B$, le vecteur $\overrightarrow{AB}$ a pour composantes $(x_b-x_a,y_b-y_a,z_b-z_a)$.

On peut écrire $\overrightarrow{OU}+\overrightarrow{UV}=\overrightarrow{OV}$ et donc $\overrightarrow{UV}=\overrightarrow{OV}-\overrightarrow{OU}$.  En remplaçant par les composantes, on obtient

$$\overrightarrow{UV}=(v_x,v_y)-(u_x,u_y)=(v_x-u_x,v_y-u_y).$$

• Dans le plan, la norme (ou longueur) du vecteur $\vec{v}$ de composantes $(v_x,v_y)$ est le nombre réel positif $\|\vec{v}\| =\sqrt{v_x^2+v_y^2}$.

Si $\vec{u}=\overrightarrow{AB}=(x_b-x_a,y_b-y_a)$ alors $\|\vec{u}\| =\|\overrightarrow{AB}\| =\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}$.

• Dans l'espace, la norme (ou longueur) du vecteur $\vec{v}$ de composantes $(v_x,v_y,v_z)$ est le nombre réel positif $\|\vec{v}\| =\sqrt{v_x^2+v_y^2+v_z^2}$.

Si $\vec{u}=\overrightarrow{AB}=(x_b-x_a,y_b-y_a,z_b-z_a)$ alors $\|\vec{u}\| =\|\overrightarrow{AB}\| =\sqrt{(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2}$.

On définit l'addition ou somme de deux vecteurs $\vec{u}$ et $\vec{v}$, comme le vecteur dont les composantes sont obtenues par addition des composantes correspondantes des deux vecteurs $\vec{u}$ et $\vec{v}$.

• Dans le plan, si $\vec{u}$ est le vecteur $(u_x,u_y)$ et $\vec{v}$ le vecteur $(v_x,v_y)$ alors le vecteur somme est le vecteur $$\overrightarrow{u+v}=(u_x+v_x,u_y+v_y).$$
• Dans l'espace, si $\vec{u}$ est le vecteur $(u_x,u_y,u_z)$ et $\vec{v}$ le vecteur $(v_x,v_y,v_z)$ alors le vecteur somme est le vecteur $$\overrightarrow{u+v}=(u_x+v_x,u_y+v_y,u_z+v_z).$$

Lorsqu'on veut soustraire le vecteur $\vec{v}$ du vecteur $\vec{u}$, on ajoute à $\vec{u}$ l'opposé de $\vec{v}$, c'est-à-dire $$\overrightarrow{u-v} = \vec{u} + (-\vec{v}).$$

• Dans le plan, si $\vec{u}$ est le vecteur $(u_x,u_y)$ et $\vec{v}$ le vecteur $(v_x,v_y)$ alors le vecteur $\overrightarrow{u-v}$ est donné par $$\overrightarrow{u-v}=(u_x-v_x,u_y-v_y).$$
• Dans l'espace, si $\vec{u}$ est le vecteur $(u_x,u_y,u_z)$ et $\vec{v}$ le vecteur $(v_x,v_y,v_z)$ alors le vecteur $\overrightarrow{u-v}$ est donné par $$\overrightarrow{u-v}=(u_x-v_x,u_y-v_y,u_z-v_z).$$

On considère le vecteur $\vec{u}$ placé en n'importe quel point du plan. On place le vecteur $\vec{v}$ à l'extrémité du vecteur $\vec{u}$. Les deux vecteurs forment alors les côtés d'un parallélogramme dont la diagonale partant de l'origine de $\vec{u}$ et arrivant à l'extrémité de $\vec{v}$ est le vecteur somme $\overrightarrow{u+v}$.

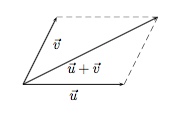
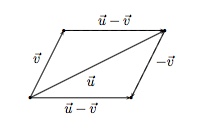
Pour soustraire $\vec{v}$ de $\vec{u}$, il suffit de placer sur le même point les origines des deux vecteurs et de prendre comme origine et extrémité du vecteur $\overrightarrow{u-v}$ respectivement l'extrémité de $\vec{v}$ et l'extrémité de $\vec{u}$.

1. L'addition vectorielle est commutative : $\vec{u} + \vec{v} = \vec{v} + \vec{u}$.
2. L'addition vectorielle est associative : $\vec{u}+(\vec{v}+\vec{w})=(\vec{u} + \vec{v}) + \vec{w}$.
3. L'addition vectorielle admet un élément neutre : $\vec{v} + \vec{o} = \vec{v}$. L'élément neutre est le vecteur nul, noté $\vec{o}$ et défini comme le vecteur dont toutes les composantes sont égales à zéro.
4. L'addition vectorielle admet un opposé : $ \vec{v} + (-\vec{v})=\vec{o}$.  Le vecteur noté $-\vec{v}$ est appelé vecteur opposé de $\vec{v}$, dont les composantes sont les composantes du vecteur $\vec{v}$, changées de signe.

Le vecteur neutre est le vecteur nul, noté $\vec{o}$, qui est tel que $\vec{u}+\vec{o}=\vec{u}$ et $\vec{o}+\vec{u}=\vec{u}$ quel que soit le vecteur $\vec{u}$. Le vecteur $\vec{o}$ est le vecteur dont toutes les composantes sont égales à zéro.

Le vecteur opposé est le vecteur $-\vec{v}$, qui est tel que $ \vec{v} + (-\vec{v})=\vec{o}$ quel que soit le vecteur $\vec{v}$. Le vecteur $-\vec{v}$ est le vecteur dont les composantes sont $(-v_x,-v_y)$.

Pour trouver le milieu d'un vecteur, on additionne les composantes de son origine et de son extrémité et on les divise par deux.

• Dans le plan, si $P = (x_p,y_p) $ et $Q = (x_q,y_q)$ alors les coordonnées du point $M$, milieu du vecteur $\overrightarrow{PQ}$ sont données par $$(x_m,y_m) =\left(\frac{1}{2} (x_p + x_q),\frac{1}{2} (y_p+ y_q)\right).$$
• Dans l'espace, si $P = (x_p,y_p,z_p) $ et $Q = (x_q,y_q,z_q)$ alors les coordonnées du point $M$, milieu du vecteur $\overrightarrow{PQ}$ sont données par $$(x_m,y_m,z_m) =\left(\frac{1}{2} (x_p + x_q),\frac{1}{2} (y_p+ y_q),\frac{1}{2} (z_p+ z_q)\right).$$

Le vecteur $\overrightarrow{UV}$ est la diagonale du parallélogramme construit sur les vecteurs $\vec{u}$ et $\vec{v}$.  Vu que dans un parallélogramme les diagonales se coupent en leur milieu, on a

$$ \begin{array}{rcl} \overrightarrow{OM}&=&\overrightarrow{OU}+\overrightarrow{UM}\\ &=&\overrightarrow{OU}+\frac{1}{2}\overrightarrow{UV}\\ &=&\overrightarrow{OU}+\frac{1}{2}(\overrightarrow{OV}-\overrightarrow{OU})\\ &=&\frac{1}{2}(\overrightarrow{OU}+\overrightarrow{OV})\ \end{array} $$

et donc $\overrightarrow{OM}=\frac{1}{2}(u_x+v_x,u_y+v_y)$.

La multiplication d'un vecteur $\vec{v}$ par un scalaire $\alpha$, notée $\alpha\vec{v}$, est le vecteur dont les composantes sont celles de $\vec{v}$ multipliées par $\alpha$.

• Dans le plan si $\vec{v}=(v_x,v_y)$ et $\alpha\in\mathbb{R}$ alors $\alpha\vec{v}=(\alpha v_x,\alpha v_y)$.
• Dans l'espace, si $\vec{v}=(v_x,v_y,v_z)$ et $\alpha\in\mathbb{R}$ alors $\alpha\vec{v}=(\alpha v_x,\alpha v_y,\alpha v_z)$.

Géométriquement, cette opération revient à effectuer une contraction ou une dilatation du vecteur $\vec{v}$, avec éventuellement un renversement de sens si le scalaire $\alpha$ est négatif.

La multiplication d'un vecteur par un scalaire possède les propriétés suivantes :

1. Cette opération est distributive par rapport à l'addition dans $\mathbb{R}$ : $(\alpha + \beta) \vec{v} = \alpha \vec{v} + \beta \vec{v}$.
2. Cette opération est distributive par rapport à l'addition vectorielle : $\alpha (\vec{u}+\vec{v}) = \alpha \vec{u} + \alpha \vec{v}$.
3. Cette opération est associative : $\alpha (\beta \vec{v}) = (\alpha \beta) \vec{v}$.
4. Cette opération possède un élément neutre : $1\cdot \vec{v} = \vec{v}$.

Deux vecteurs sont colinéaires ou parallèles s'ils ont la même direction, c'est-à-dire s'il existe $\alpha\in\mathbb{R}$ tel que $\vec{u}=\alpha\vec{v}$.

Deux vecteurs ont la même direction et sont de même sens si $\vec{u}=\alpha\vec{v}$, pour un certain $\alpha>0$.

Deux vecteurs ont la même direction et sont de sens contraire si $\vec{u}=\alpha\vec{v}$, pour un certain $\alpha<0$.

Deux vecteurs sont parallèles s'il existe $\alpha\in\mathbb{R}$ tel que $\vec{u}=\alpha\vec{v}$, c'est-à-dire s'ils sont multiples l'un de l'autre.

Le produit scalaire est une opération de multiplication entre deux vecteurs donnant comme résultat un nombre. Il est noté en général avec un point $\vec{u}\cdot\vec{v}$. Pour le distinguer de la multiplication usuelle, nous le noterons $\vec{u}\odot\vec{v}$. Le produit scalaire de deux vecteurs est égal à la somme des produits de leurs composantes correspondantes.

• Dans le plan, si $\vec{u}=(u_x,u_y)$ et $\vec{v}=(v_x,v_y)$ alors $\vec{u}\odot\vec{v}=u_x v_x + u_y v_y.$
• Dans l'espace, si $\vec{u}=(u_x,u_y,u_z)$ et $\vec{v}=(v_x,v_y,v_z)$ alors $\vec{u}\odot\vec{v}=u_x v_x + u_y v_y + u_z v_z.$

1. Le produit scalaire d'un vecteur avec lui-même est égal au carré de sa norme : $\vec{v}\odot\vec{v}=\|\vec{v}\|^2$.
2. Le produit scalaire de deux vecteurs est commutatif : $\vec{u}\odot\vec{v}=\vec{v}\odot\vec{u}$.
3. Il y a distributivité du produit scalaire par rapport à l'addition des vecteurs : $\vec{u}\odot(\vec{v}+\vec{w})=\vec{u}\odot\vec{v}+\vec{u}\odot\vec{w}$.
4. Il y a associativité mixte : $(\alpha\vec{u})\odot\vec{v}=\alpha(\vec{u}\odot\vec{v})=\vec{u}\odot(\alpha\vec{v})$.
5. Le vecteur nul est absorbant pour le produit scalaire : $\vec{o}\odot\vec{u}=0$.

Si $\theta$ désigne l'angle entre les deux vecteurs non nuls $\vec{u}$ et $\vec{v}$, alors

$$\vec{u}\odot\vec{v}=\|\vec{u}\|\|\vec{v}\|\cos\theta.$$

Si $\theta$ désigne l'angle entre les deux vecteurs non nuls $\vec{u}$ et $\vec{v}$, alors

$$\cos\theta =\displaystyle\frac{\vec{u}\odot\vec{v}}{\|\vec{u}\|\|\vec{v}\|}.$$

Travaillons dans l'espace. Soit $\vec{u}=(u_x,u_y,u_z)$ et $\vec{v}=(v_x,v_y,v_z)$.

Cas 1 : Les vecteurs $\vec{u}$ et $\vec{v}$ ne sont pas colinéaires.

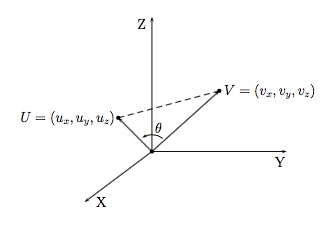
La Règle des cosinus permet d'écrire

$$\|\overrightarrow{UV}\|^2=\|\vec{u}\|^2+\|\vec{v}\|^2-2\|\vec{u}\|\|\vec{v}\|\cos\theta.$$

D'où

$$(v_x-u_x)^2 + (v_y-u_y)^2 + (v_z-u_z)^2=(u_x^2+u_y^2+u_z^2)+(v_x^2+v_y^2+v_z^2)-2\|\vec{u}\|\|\vec{v}\|\cos\theta.$$

On peut simplifier cette dernière expression en

$$-2u_xv_x-2u_yv_y-2u_zv_z=-2\|\vec{u}\|\|\vec{v}\|\cos\theta,$$

ce qui par division des deux membres par $-2$ donne le résultat recherché.

Cas 2 : Les vecteurs $\vec{u}$ et $\vec{v}$ sont colinéaires, c'est-à-dire il existe $\alpha\in \mathbb{R}$ tel que $\vec{v} = \alpha\vec{u}$.

On a en vertu des propriétés du produit scalaire,

$$\vec{u}\odot\vec{v}=\vec{u}\odot(\alpha\vec{u})=\alpha(\vec{u}\odot\vec{u})=\alpha\|\vec{u}\|^2.$$

De même, on a

$$\|\vec{u}\|\|\vec{v}\|\cos\theta=\|\vec{u}\|\|\alpha\vec{u}\|\cos\theta=|\alpha|\|\vec{u}\|^2\cos\theta.$$

Si $\alpha>0$, alors $|\alpha|=\alpha$, $ \theta=0$ et $|\alpha|\|\vec{u}\|^2\cos\theta=\alpha\|\vec{u}\|^2=\vec{u}\odot\vec{v}$.

Si $\alpha<0$, alors $|\alpha|=-\alpha$, $\theta=\pi$ et $|\alpha|\|\vec{u}\|^2\cos\theta=-\alpha\|\vec{u}\|^2\cdot(-1)=\alpha\|\vec{u}\|^2=\vec{u}\odot\vec{v}$.

Deux vecteurs sont orthogonaux s'ils forment un angle droit.

Deux vecteurs sont orthogonaux s'ils forment un angle droit.  Dans ce cas, le cosinus de l'angle vaut $0$ et on obtient $\vec{u}\odot\vec{v}=\|\vec{u}\|\|\vec{v}\|\cos 90^°=0$.  Donc

$$\vec{u}\perp\vec{v}\Leftrightarrow\vec{u}\odot\vec{v}=0.$$

Soient deux vecteurs $\vec{u}$ et $\vec{v}$. Supposons ces deux vecteurs placés à l'origine et soit $P$ le point où la droite passant par l'extrémité de $\vec{v}$ et perpendiculaire à la direction de $\vec{u}$ rencontre la droite contenant le vecteur $\vec{u}$.

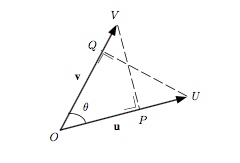
Le vecteur $\overrightarrow{OP}$ est la projection orthogonale du vecteur $\vec{v}$ sur le vecteur $\vec{u}$. Le sens de $\overrightarrow{OP}$ par rapport à $\vec{u}$ dépendra de l'angle $\theta$. Il est le même si l'angle n'excède pas $90^\circ$.

On appelle composante d'un vecteur $\vec{v}$ suivant un vecteur $\vec{u}$, la quantité $\|\vec{v}\|\cos\theta$. Il s'agit d'un nombre et non pas d'un vecteur. C'est la longueur du vecteur qui est la projection orthogonale de $\vec{v}$ sur $\vec{u}$ si cette projection orthogonale a le même sens que $\vec{u}$, l'opposé de cette longueur dans le cas contraire.

On note $\mbox{comp}_u\vec{v}$ la composante du vecteur $\vec{v}$ suivant le vecteur $\vec{u}$.  C'est la longueur du vecteur qui est la projection orthogonale de $\vec{v}$ sur $\vec{u}$ si cette projection orthogonale a le même sens que $\vec{u}$, l'opposé de cette longueur dans le cas contraire.

On a

$$\mbox{comp}_u\vec{v}=\|\overrightarrow{OP} \|=\|\vec{v}\|\cos{\theta}=\|\vec{v}\|\cdot \dfrac{\vec{u}\odot\vec{v}}{\|\vec{u}\|\cdot \|\vec{v}\|}$$

et donc

$$\mbox{comp}_u\vec{v}=\displaystyle\frac{\vec{u}\odot\vec{v}}{\|\vec{u}\|}.$$

Inégalité de Cauchy-Schwartz : Si $\vec{u}$ et $\vec{v}$ sont deux vecteurs alors $|\vec{u}\odot\vec{v}|\le \|\vec{u}\|\|\vec{v}\|$.

Démonstration : En utilisant l'interprétation géométrique du produit scalaire, on obtient
$$ \begin{array}{rcl} |\vec{u}\odot \vec{v}|&=&|\, \|\vec{u}\|\|\vec{v}\|\cos{\theta}|\\ &=&\|\vec{u}\|\|\vec{v}\||\cos{\theta}|\\ &\leq&\|\vec{u}\|\|\vec{v}\|. \end{array} $$

Inégalité triangulaire : Si $\vec{u}$ et $\vec{v}$ sont deux vecteurs alors $\|\vec{u}+\vec{v}\|\le\|\vec{u}\|+\|\vec{v}\|$.

Démonstration : En utilisant l'inégalité de Cauchy-Schwartz et les propriétés du produit scalaire, on obtient

$$ \begin{array}{rcl} \|\vec{u}+\vec{v}\|^2&=&(\vec{u}+\vec{v})\odot (\vec{u}+\vec{v})\\ &=&\vec{u}\odot \vec{u}+\vec{u}\odot \vec{v}+\vec{v}\odot \vec{u}+\vec{v}\odot \vec{v}\\ &=&\|\vec{u}\|^2+2\, \vec{u}\odot \vec{v}+\|\vec{v}\|^2\\ &\leq&\|\vec{u}\|^2+2\, \|\vec{u}\|\, \|\vec{v}\|+\|\vec{v}\|^2\\ &=&(\|\vec{u}\|+\|\vec{v}\|)^2. \end{array} $$

En prenant la racine carrée des deux membres (qui sont positifs), on trouve $\|\vec{u}+\vec{v}\|\le\|\vec{u}\|+\|\vec{v}\|$.

Cette inégalité spécifie que dans un triangle, la longueur d'un côté ne peut dépasser la somme des longueurs des deux autres côtés.

Le produit vectoriel est une opération de multiplication entre deux vecteurs donnant comme résultat un vecteur. Il est noté $\vec{u}\times\vec{v}$ (ou encore $\vec{u}\wedge\vec{v}$).

Le produit vectoriel de deux vecteurs $\vec{u}$ et $\vec{v}$ est le vecteur $\vec{u}\times\vec{v}$ qui possède les caractéristiques suivantes :

• direction : $\vec{u}\times\vec{v}$ est perpendiculaire à $\vec{u}$ et à $\vec{v}$;
• sens : les vecteurs $\vec{u}$, $\vec{v}$ et $\vec{u}\times\vec{v}$ pris dans cet ordre forment un repère d'orientation directe;
• longueur : $\|\vec{u}\times\vec{v}\|=\|\vec{u}\|\|\vec{v}\|\, |\sin{\theta}| $.

1. Le produit vectoriel de deux vecteurs est anti-commutatif : $\vec{u}\times\vec{v}=-(\vec{v}\times\vec{u}).$
2. Le produit vectoriel est linéaire à gauche : $\vec{u}\times(\alpha\vec{v}+\beta\vec{w})=\alpha(\vec{u}\times\vec{v})+\beta(\vec{u}\times\vec{w}).$
3. Le produit vectoriel est linéaire à droite : $(\alpha\vec{u}+\beta\vec{v})\times\vec{w}=\alpha(\vec{u}\times\vec{w})+\beta(\vec{v}\times\vec{w}).$

!! Attention : Le produit vectoriel n'est pas commutatif ni associatif.

Soit $\vec{u}=(u_x,u_y,u_z)$ et $\vec{v}=(v_x,v_y,v_z)$. Les composantes du vecteur $\vec{u}\times\vec{v}$ sont données par

$$\vec{u}\times\vec{v}=(u_yv_z-u_zv_y,u_zv_x-u_xv_z, u_xv_y-u_yv_x).$$

La longueur $\|\vec{u}\times\vec{v}\|$ est l'aire du parallélogramme construit sur les vecteurs $\vec{u}$ et $\vec{v}$.

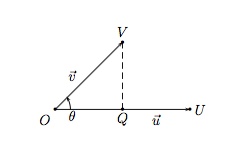
Soit $Q$ la projection orthogonale de $V$ sur $\vec{u}$.  La longueur $\|\overrightarrow{QV}\|$ représente la hauteur du parallélogramme construit sur $\vec{u}$ et $\vec{v}$.

L'aire de ce parallélogramme est donc donnée par $\|\vec{u}\|\cdot\|\overrightarrow{QV}\|$ et comme

$$|\sin{\theta}|=\frac{\|\overrightarrow{QV}\|}{\|\overrightarrow{OV}\|}=\frac{\|\overrightarrow{QV}\|}{\|\vec{v}\|},$$

on obtient

$$\mbox{Aire}=\|\vec{u}\|\, \|\vec{v}\|\, |\sin{\theta}|=\|\vec{u}\times\vec{v}\|.$$

Deux vecteurs sont colinéaires s'ils forment un angle droit ou plat.  Dans ce cas, le sinus de l'angle vaut $0$ et puisque $\|\vec{u}\times\vec{v}\|=\|\vec{u}\|\|\vec{v}\|\, |\sin{\theta}| $ on en déduit que le produit vectoriel est nul.  Donc

$$\vec{u}\parallel\vec{v}\Leftrightarrow\vec{u}\times\vec{v}=\vec{o}.$$

Si on dispose de 3 vecteurs donnés $\vec u, \vec v $ et $\vec w $, le produit mixte est donné par $(\vec u \times \vec v) \odot \vec w .$

Dans un repère cartésien orthonormé, le nombre $| (\vec u \times \vec v) \odot \vec w |$ est le volume du parallélipipède construit sur les vecteurs $\vec u$, $\vec v$ et $\vec w$ (où $\vec u$ et $\vec v$ déterminent la base du parallélipipède).

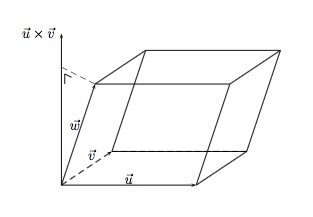
Si nous regardons le parallélipipède construit sur les 3 vecteurs $\vec u$, $\vec v $ et $\vec w$, nous observons que

• $\| \vec u \times \vec v \|$ donne l'aire de la base (construite sur $\vec u$ et $\vec v$)
• $\|\vec w \| |\cos (\vec u \times \vec v, \vec w)|$ donne la longueur de la projection orthogonale de $\vec w $ sur la droite qui porte $\vec u \times \vec v$, c'est-à-dire la hauteur du parallélipipède

Donc $|(\vec u \times \vec v) \odot \vec w|$ donne le volume du parallélipipède.